Extending Example 7-6, the correlation between Southeast Utilities and Precision Instruments returns is +0.29. In order to focus on the effects of a changing correlation coefficient, we continue to assume weights of 0.5 each—50 percent is placed in each security. Summarizing the data in this example,

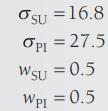
With these data, the standard deviation (risk) for this portfolio, 

since 2(0.5)(0.5)(16.8)(27.5) = 229.32. 

The risk of this portfolio clearly depends heavily on the value of the third term, which in turn depends on the correlation coefficient between the returns for SU and PI. To assess the potential impact of the correlation, consider the following cases: a ρ of +1, +0.5, +0.29, 0, −0.5, and −1.0. Calculating portfolio risk under each of these scenarios produces the following portfolio risks:

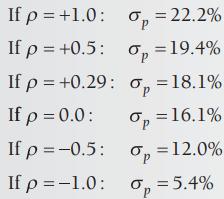
These calculations clearly show the impact that combining securities with less than perfect positive correlation has on portfolio risk. The risk of the portfolio steadily decreases from 22.2 percent to 5.4 percent as the correlation coefficient declines from +1.0 to −1.0. Note, however, that risk declines from 22.2 percent to only 16.1 percent as the correlation coefficient drops from +1 to 0 and it is only cut in half (approximately) when is −0.5. 

Example 7-6

Consider the returns between Southeast Utilities and Precision Instruments for the period 2005–2014. The summary statistics for these two stocks are as follows:

Assume, for expositional purposes, we place equal amounts in each stock; therefore, the weights are 0.5 and 0.5: 

Su = 16.8 SU OPI = 27.5 Opi WSU = 0.5 WPI = 0.5