Write a method for solving a quadratic equation using the following header:

public static int solveQuadratic(double[] eqn, double[] roots)

The coefficients of a quadratic equation ax² + bx + c = 0 are passed to the array eqn and the real roots are stored in roots. The method returns the number of real roots. See Programming Exercise 3.1 on how to solve a quadratic equation.

Write a program that prompts the user to enter values for a, b, and c and displays the number of real roots and all real roots.

The two roots of a quadratic equation?ax2 +?bx?+?c?= 0 can be obtained using the following formula:

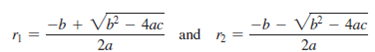
b2 - 4ac is called the discriminant of the quadratic equation. If it is positive, the equation has two real roots. If it is zero, the equation has one root. If it is negative, the equation has no real roots.

Write a program that prompts the user to enter values for a, b, and c and displays the result based on the discriminant. If the discriminant is positive, display two roots. If the discriminant is 0, display one root. Otherwise, display ?The equation has no real roots?.

Note that you can use Math.pow(x, 0.5) to compute ?x. ? Here are some sample runs.

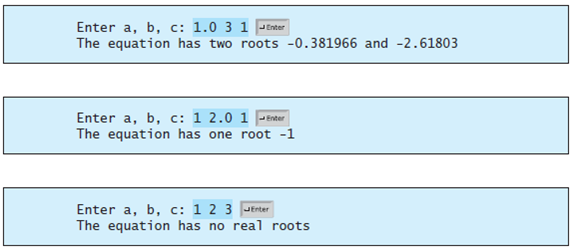
-b - VB - 4ac 2a -b + VB 4ac and n= 2a Enter a, b, c: 1.0 3 1 The equation has two roots -0.381966 and -2.61803 Enter Enter a, b, c: 1 2.0 1 PEnter The equation has one root -1 Enter a, b, c: 1 2 3 JErter The equation has no real roots