Show that every eigenvalue of such a matrix is necessarily real Let A be an n n real matrix with the property that A T A, let x be any vector in C n , and let q X T Ax The equalities below show that q is a real number by verifying that q q Give a reason for each step q x Ax xAx xAX (xAx) xA x q (a) (b) (c) (d) (e)

Question: Show that every eigenvalue of such a matrix is necessarily real. Let A be an n n real matrix with the property that A

Show that every eigenvalue of such a matrix is necessarily real.

Let A be an n × n real matrix with the property that A^T = A, let x be any vector in Cⁿ, and let q = X̅^T Ax. The equalities below show that q is a real number by verifying that q̅ = q. Give a reason for each step.

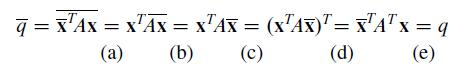
q = x Ax = xAx = xAX = (xAx) = xA

q = x Ax = xAx = xAX = (xAx) = xA x = q (a) (b) (c) (d) (e)

Step by Step Solution

★★★★★

3.32 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a properties of conjugates and the fa... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Linear Algebra And Its Applications Questions!

FINA 480 Case assignment #2 Clarkson Lumber Company This case is an investigation of short-term debt financing decisions. You are asked to write up a professional memo representing either Mr....

Let A be an n x n real matrix with the property that AT = A, let x be any vector in Cn, and let q = xrAx. The equalities below show that q is a real number by verifying that q = q. Give a reason for...

Let B be an n x n matrix. Suppose AB = 0 for some nonzero m n matrix A. Show that no n n matrix C exists such that BC = I.

Let W be an n 1 matrix such that WT W = 1. The n n matrix H = In - 2WWT is called a Householder* matrix. (a) Show that H is symmetric. (b) Show that H-1 = HT.

An n x n complex matrix A is called skew-hermitian if and only if: A = -A. A real, skew-hermitian matrix is called anti-symmetric or skew-symmetric. a) Let A be a skew-hermitian matrix and suppose A...

HEY CAN YOU HELP ME SOLVE THE FOLLOWING QUESTIONS: 63, 65, 73, 81, 82, 83 5.3 Diagonalization of Matrices 323 57. [_7 3]: ([:] . ): 43 74. Find a 2 x 2 matrix having eigenvalues 7 and -4, with 58. 2...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Only 18 and 19 please 4.4 Eigenvalues and the Characteristic Polynomial 305 ultimately requires the evaluation of al/2 determinants of order (2 x 2). Even for modest values of n. the number a!/2 is...

As we saw in class, eigenvalues and eigenvectors of an arbitrary square matrix A are not necessarily well-behaved. In particular, it is possible for A to have complex eigenvalues/eigenvectors or even...

Eigenvalue/Eigenvector Part IV: Suppose A is an n x n matrix. a. What does it mean to say that a vector x E Rn is an eigenvector of A? b. Suppose A E R is an eigenvalue of A. What is the eigenspace...

1 1. (6+4+4+6) Let P3 denote the vector space of all third degree or less polynomials. (a) Find two linearly independent vectors in P3 that interpolate the data points (1, 2), (2, 1) and (3, 2). (b)...

Mel Snow is the manager of a firm, Taxation Matters, which specialises in the preparation of income tax returns. The firm offers two basic products: the preparation of income tax returns for wage and...

A spring is stretched 0.1 m by a force of 3 N. A mass of 2 kg is hung from the spring and is also attached to a damper that exerts a force of 3 N when the velocity of the mass is 5 m/s. If the mass...

16. Describe the major controls for cash receipts.

30. Consider a graph with nodes 1, 2, . . . , n and the n 2 arcs (i, j), i = j, i, j,= 1, . . . , n. (See Section 3.6.2 for appropriate definitions.) Suppose that a particle moves along this graph...

The following data describe fuel consumption and flying hours for turboprop general aviation aircraft from 1992 through 1997. Fuel consumption is in millions of gallons; flying time is in millions of...

The following data describe U.S. passenger car travel and fuel consumption from 1995 through 1999. The data represent billions of gallons consumed and billions of miles traveled, respectively. a....

As part of its ongoing testing and reporting program, The Insurance Institute for Highway Safety crashes vehicles into fixed objects at low speeds, then records the cost of repairs necessary to fix...

At December 31, before adjusting and closing the accounts had occurred, the Allowance for Doubtful Accounts of Seaboard Corporation showed a debit balance of $4,000. An aging of the accounts...

4-7.) What is meant by the term equivalent units of production when the weighted-average method is used? 5-1.) Distinguish between(a) variable cost, (b) a fixed cost, and (c) a mixed cost. 5-2.) What...

Lido Co. manufactures A and B from a joint process with a cost of $80,000. 5,000 pounds of A can be sold at split-off for $20 per pound or processed further at additional cost of $20,000 and then...