Question: Partitioning large square matrices can sometimes make their inverses easier to compute, particularly if the blocks have a nice form. Verify by block multiplication that
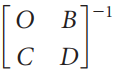
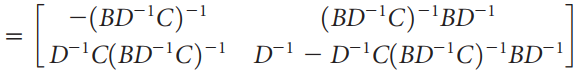
-1 B [c D. -(BD'C)-! D'C(BD-'C)-! D' D-C(BD'C)-'BD" ! (BD'C)-'BD'
Step by Step Solution
3.43 Rating (159 Votes )
There are 3 Steps involved in it
BD BBCDDC BDC DDC B... View full answer

Get step-by-step solutions from verified subject matter experts


