Question: Partitioning large square matrices can sometimes make their inverses easier to compute, particularly if the blocks have a nice form. Verify by block multiplication that

Partitioning large square matrices can sometimes make their inverses easier to compute, particularly if the blocks have a nice form. Verify by block multiplication that the inverse of a matrix, if partitioned as shown, is as claimed. (Assume that all inverses exist as needed.)

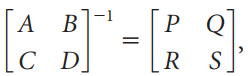
A B P Q %D

Where P = (A - BD^-1 C)^-1,
Q = -PBD^-1, R = -D^-1CP, and S = D^-1 + D^-1CPBD^-1

A B P Q %D

Step by Step Solution

★★★★★

3.45 Rating (174 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

ABA B A C D C D A B P Q C D RS 3 CP P AP ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Linear Algebra Questions!

Verify by direct multiplication that the following matrices are inverses, i.e., both conditions in (1.36) hold: (a) (b) (c) 112 213 321 122 3 3-78-7

Compute the following using block multiplication (all blocks are k Ã k). (a) (b) (c) 0 1 0 I 1 0 | , any 7121

Blocks A and B each have a mass of 0.4 kg and block C has a mass of 1.2 kg. The coefficient of friction between the blocks and the plane is k = 0.30. Initially block A is moving at a speed v0 = 3 m/s...

Partitioning large square matrices can sometimes make their inverses easier to compute, particularly if the blocks have a nice form. In Exercises, verify by block multiplication that the inverse of a...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS The purpose of this chapter is to introduce you to matrix algebra, which has many applications. You are already familiar with several algebras:...

Jones & Bartlett Learning, LLC. NOT FOR RESALE OR DISTRIBUTION CHAPTER Hot Spot Analysis 10 LEARNING OBJECTIVES C A R R Provide a working definition of a \"hot spot.\" , Be able to explain different...

Python and most Python libraries are free to download or use, though many users use Python through a paid service. Paid services help IT organizations manage the risks associated with the use of...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

On January 1, 2021, a company began the policy of giving each of its 75 employees 12 days of vacation each year. The vacation accumulates such that unused vacation days can be carried over from year...

List and label the different types of variables at the following case: explain and illustrate by diagrams the relationships among the variables : A manager of an insurance company finds that fear...

A graph of percentage increases in the money supply and average annual increases in the price level for various countries provides evidence that a. changes in the two variables are exactly equal. b....

=+2. What sort of demographic factors might lead to greater air travel in the future?

What is the difference between a between- groups research design and a within-groups research design?

Lets assume the average speed of a serve in mens tennis is around 135 mph, with a standard deviation of 6.5 mph. Because these statistics are calculated over many years and many players, we will...

In an exercise in Chapter 7, we asked whether college football teams tend to be more likely or less likely to be mismatched in the upper National Collegiate Athletic Association (NCAA) divisions....

Exercise 9. (10pts) Selecting a Jury The grade appeal process at a university requires that a jury be structured by selecting five individuals ran- domly from a pool of eight students and ten...

Type 2D: You are a consultant to a firm evaluating an expansion of its current business. The cash-flow forecasts (in millions of dollars) for the project are as follows. Year 0: initial outlay of...

An oil drilling company must choose between two mutually exclusive extraction projects, and each costs $12.8 million. Under Plan A, all the oil would be extracted in 1 year, producing a cash flow at...