Consider the production function given in Problem 3. Assume that \(N\) is constant and equal to 

1 . Note that if \(z=x^{a}\), then \(g_{z} \approx a g_{x}\), where \(g_{z}\) and \(g_{x}\) are the growth rates of \(z\) and \(x\).

a. Given the growth approximation here, derive the relation between the growth rate of output and the growth rate of capital.

b. Suppose we want to achieve output growth equal to \(2 \%\) per year. What is the required rate of growth of capital?

c. In part b, what happens to the ratio of capital to output over time?

d. Is it possible to sustain output growth of \(2 \%\) forever in this economy? Why or why not?

Data from Problem 3

Consider the production function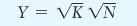

Y = VK VN