Consider a self-financing trading strategy of a portfolio with a dividend paying asset and a money market account over the time horizon [0,T ]. Under the risk neutral measure Q, let the dynamics of the asset price S_t be governed by

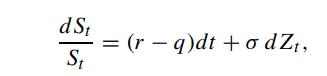
where q is the dividend yield, q = r. We adopt the trading strategy of holding nt units of the asset at time t, where 

Let X_t denote the portfolio value at time t, whose dynamics is then given by

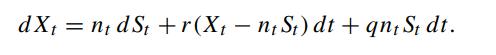
The initial portfolio value X₀ is chosen to be

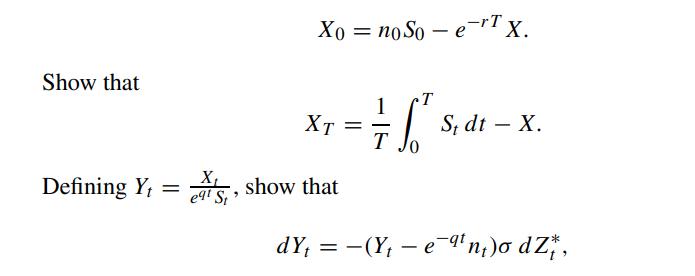
where Z^∗_t = Z_t − σt is a Brownian process under Q^∗-measure with e^qtS_t as the numeraire. Note that the price function of the fixed strike Asian call option with strike X is given by

with u(y,T ) = max(y, 0).

Transcribed Image Text:

d St St (r-q)dt + od Zt,