Let the exit time density q⁺(t; x₀,t₀) have dependence on the initial state X(t₀) = x₀. We write τ = t − t₀ so that q⁺(t; x₀,t₀) = q⁺(x₀,τ). Show that the partial differential equation formulation is given by

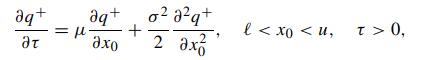
with auxiliary conditions:

Solve for q⁺(x₀,τ) using the partial differential equation approach and compare the solution with that given in (4.1.53b). Also, show that

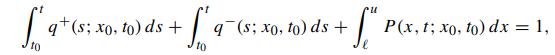
where P(x,t; x₀,t₀) is the transition density function defined in Problem 4.9.

Problem 4.9.

Let P(x,t; x₀,t₀) denote the transition density function of the restricted Brownian process W^μ_t = μt + σZ_t with two absorbing barriers at x = 0 and x = ℓ. Using the method of separation of variables (Kevorkian, 1990), show that the solution to P(x,t; x₀,t₀) admits the following eigen-function expansion [which differs drastically in analytic form from that in (4.1.48)]

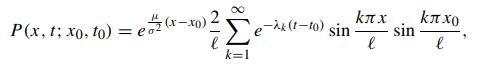
where the eigenvalues are given by

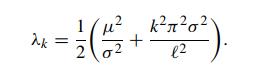P(x,t; x₀,t₀) satisfies the forward Fokker–Planck equation with auxiliary conditions: P(0,t) = P(ℓ,t) = 0 and P(x,t⁺₀ ; x₀,t₀) = δ(x−x₀). 

Pelsser (2000) derived the above solution by performing the Laplace inversion using Bromwich contour integration. 

Transcribed Image Text:

əq+ Әт = н aq+ 02 02q+ Әxo 2 аха + l < xo < u, T > 0,