We would like to price the floor on the composition defined in Problem 8.22 using the LIBOR
Question:
We would like to price the floor on the composition defined in Problem 8.22 using the LIBOR Market model. Now, we assume that the LIBOR Li(t) follows the arithmetic Brownian process:
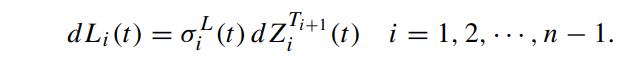
Problem 8.22
Consider a floor on composition, where the composition is defined as
![n-1 ][(1+&+1Li). i=1](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/6/3/7/932655dacec3703a1700637931667.jpg)
Here, Li is reset at time Ti and αi+1 is the accrual factor over the time interval (Ti,Ti+1]. The payment of this floor at maturity Tn is
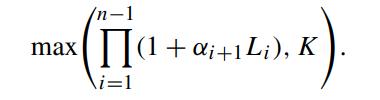
Assuming that the discounted bond price process follows the same process as in Problem 8.21, show that the time-0 value of this floor on composition is given by (Henrard, 2005)
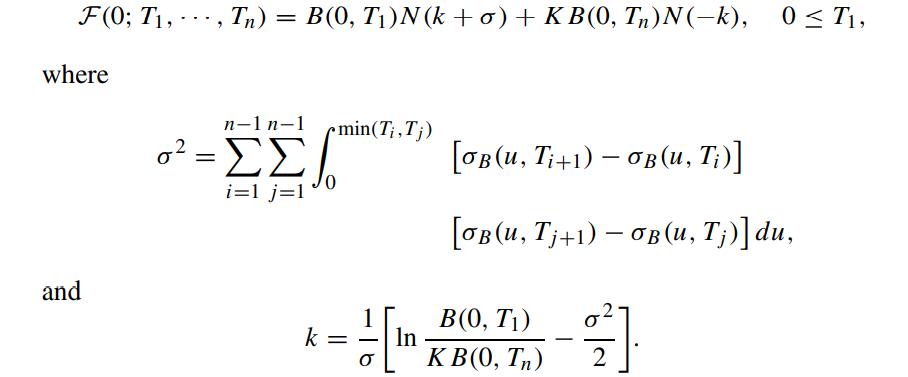 Problem 8.21
Problem 8.21
Assume that the T-maturity discounted bond price process B(t,T) follows the one-factor Gaussian HJM under the risk neutral measure Q:
 A caption is a call option on a cap, whose terminal payoff at time T is given by
A caption is a call option on a cap, whose terminal payoff at time T is given by
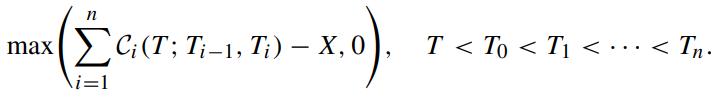
Here, Ci(T ; Ti−1,Ti) is the time-T value of a caplet with payment on the LIBOR Li−1 at time Ti and X is the strike price, i = 1, 2, ··· ,n. Since a cap can be visualized as a series of put options on the zero-coupon bonds, a caption is seen as a compound call on a put. By applying Jamshidian’s decomposition technique (Jamshidian, 1989) for an option on a coupon-bearing bond, find the time-t value of the caption, t
Use the identity
![n-1 B(u, Th) B(u, T;) = B(u, Tj+1) B(u,T;)] j=1 to show that = i=1 Ti [B(u, Ti+1) B(u, T;)] [2B(u, T)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/6/3/8/273655dae4175e4c1700638272844.jpg)
Here, σLi (t) is the deterministic volatility function and ZTi+1i (t) is QTi+1- Brownian. By making the “frozen coefficient” assumption in the drift term of the stochastic differential equation of Li(t) under the terminal measure QTn , show that the time-0 value of the floor on composition is given by (Henrard, 2005)
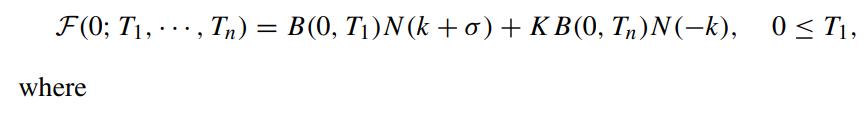

αi+1 is the accrual factor of (Ti,Ti−1), i = 1, 2, ··· ,n − 1, and the (i, j)th entry of the matrix S is given by
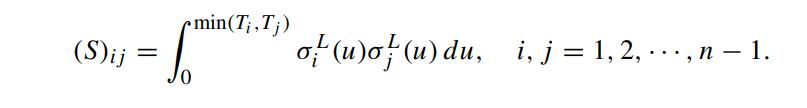
Step by Step Answer:






