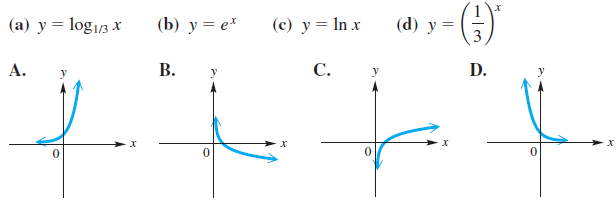
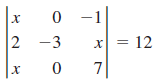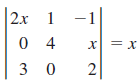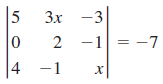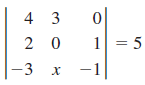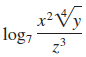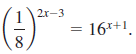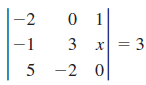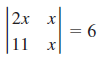New Semester
Started
Get
50% OFF
Study Help!
--h --m --s
Claim Now
Question Answers
Textbooks
Find textbooks, questions and answers
Oops, something went wrong!
Change your search query and then try again
S
Books
FREE
Study Help
Expert Questions
Accounting
General Management
Mathematics
Finance
Organizational Behaviour
Law
Physics
Operating System
Management Leadership
Sociology
Programming
Marketing
Database
Computer Network
Economics
Textbooks Solutions
Accounting
Managerial Accounting
Management Leadership
Cost Accounting
Statistics
Business Law
Corporate Finance
Finance
Economics
Auditing
Tutors
Online Tutors
Find a Tutor
Hire a Tutor
Become a Tutor
AI Tutor
AI Study Planner
NEW
Sell Books
Search
Search
Sign In
Register
study help
mathematics
college algebra
College Algebra 12th edition Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels - Solutions
Evaluate the sum. k=1
Evaluate the sum. i-1 4 i=1
Evaluate the sum. i-1 3 4, i=1
Evaluate the sum. + + + 3.
Evaluate the sum. 2 4 6 27
Evaluate the sum.100 + 10 + 1 + · · ·
Evaluate the sum. 18 + 6 + 2 +=+ 3
We determined that 1 + 1/3 + 1/9 + 1/27 + · · · converges to 3/2 using an argument involving limits. Use the formula for the sum of the terms of an infinite geometric sequence to obtain the same result.
Work each problem.Useto show that 2 + 1 + 1/2 + 1/4 + · · · converges to 4. lim S. п
Find r for each infinite geometric sequence. Identify any whose sum diverges.625, 125, 25, 5, . . .
Find r for each infinite geometric sequence. Identify any whose sum diverges.-48, -24, -12, -6, . . .
Find r for each infinite geometric sequence. Identify any whose sum diverges.2, -10, 50, -250, . . .
Find r for each infinite geometric sequence. Identify any whose sum diverges.12, 24, 48, 96, . . .
The number 0.999c can be written as the sum of the terms of an infinite geometric sequence: 0.9 + 0.09 + 0.009 + · · · . Here we have a1 = 0.9 and r = 0.1. Use the formula for S∞ to find this sum. Does intuition indicate that this answer is correct?
Under what conditions does the sum of an infinite geometric series exist?
Evaluate the sum. Σ3 k=3
Evaluate the sum. 10 2k k=4
Evaluate the sum. Σ 243| 3 j=1
Evaluate the sum. 48 j=1
Evaluate the sum. 4 Σ(-2) i=1
Evaluate the sum. -3)' i=1
Use the formula for Sn to find the sum of the first five terms of the geometric sequence.a1 = -3.772, r = -1.553
Use the formula for Sn to find the sum of the first five terms of the geometric sequence.a1 = 8.423, r = 2.859
Use the formula for Sn to find the sum of the first five terms of the geometric sequence. 12, -4, 4 4 3
Use the formula for Sn to find the sum of the first five terms of the geometric sequence. 9. 18, -9,
Use the formula for Sn to find the sum of the first five terms of each geometric sequence.4, 16, 64, 256, . . .
Use the formula for Sn to find the sum of the first five terms of the geometric sequence.2, 8, 32, 128, . . .
Determine r and a1 for the geometric sequence. 100 аз 3 300, а, 243
Determine r and a1 for each geometric sequence.a3 = 50, a7 = 0.005
Determine r and a1 for each geometric sequence. a4 4 128 ag
Determine r and a1 for each geometric sequence. аз — 5, ag 625
Determine r and a1 for each geometric sequence.a2 = -8, a7 = 256
Determine r and a1 for each geometric sequence.a2 = -6, a7 = -192
Determine a5 and an for each geometric sequence. 9 27 81 3, 4' 16' 64
Determine a5 and an for each geometric sequence. 5 10, -5, 2'
Determine a5 and an for each geometric sequence. 1 2 8 32 2'3'9' 27'
Determine a5 and an for each geometric sequence. 4 25 5. 2, 5, - 2
Determine a5 and an for each geometric sequence.-2, 6, -18, 54, . . .
Determine a5 and an for each geometric sequence.-4, -12, -36, -108, . . .
Determine a5 and an for each geometric sequence.a4 = 18, r = 2
Determine a5 and an for each geometric sequence.a4 = 243, r = -3
Determine a5 and an for each geometric sequence.a3 = -2, r = 4
Determine a5 and an for the geometric sequence.a2 = -4, r = 3
Determine a5 and an for each geometric sequence.a1 = 8, r = -5
Determine a5 and an for each geometric sequence.a1 = 5, r = -2
Recall from the beginning of this section that an employee agreed to work for the following salary: $0.01 the first day, $0.02 the second day, $0.04 the third day, $0.08 the fourth day, and so on, with wages doubling each day. Determine (a) the amount earned on the day indicated and (b) the total
Recall from the beginning of this section that an employee agreed to work for the following salary: $0.01 the first day, $0.02 the second day, $0.04 the third day, $0.08 the fourth day, and so on, with wages doubling each day. Determine (a) the amount earned on the day indicated and (b) the total
Recall from the beginning of this section that an employee agreed to work for the following salary: $0.01 the first day, $0.02 the second day, $0.04 the third day, $0.08 the fourth day, and so on, with wages doubling each day. Determine (a) the amount earned on the day indicated and (b) the total
Recall from the beginning of this section that an employee agreed to work for the following salary: $0.01 the first day, $0.02 the second day, $0.04 the third day, $0.08 the fourth day, and so on, with wages doubling each day. Determine (a) the amount earned on the day indicated and (b) the total
whether each sequence is arithmetic, geometric, or neither. If it is arithmetic, give the common difference, d. If it is geometric, give the common ratio, r. 8, 2,
Write an equation for the conic section.Ellipse with foci at (-3, 3) and (-3, 11); major axis of length 10
whether each sequence is arithmetic, geometric, or neither. If it is arithmetic, give the common difference, d. If it is geometric, give the common ratio, r.5, 10, 20, 35, . . .
whether each sequence is arithmetic, geometric, or neither. If it is arithmetic, give the common difference, d. If it is geometric, give the common ratio, r. 1 2 3 4 3'3'3'3
whether each sequence is arithmetic, geometric, or neither. If it is arithmetic, give the common difference, d. If it is geometric, give the common ratio, r.4, -8, 16, -32, . . .
Fill in the blank to correctly complete each sentence.When evaluated, Σ81 (3. is i=1
Fill in the blank to correctly complete each sentence.The sum of the first five terms of the geometric sequence 5, 10, 20, 40, . . . is ______.
Fill in the blank to correctly complete each sentence.For the geometric sequence with nth term an = 4 (1/2)n-1, the term a5 = ______.
Fill in the blank to correctly complete each sentence.For the geometric sequence having a1 = 6 and r = 2, the term a3 = _________.
Fill in the blank to correctly complete each sentence.The common ratio for the sequence -25, 5, -1, 1/5, . . . . is __________.
Fill in the blank to correctly complete each sentence.In a geometric sequence, each term after the first is obtained by multiplying the preceding term by a fixed nonzero real number called the common _______.
Solve the problem.Is the sequence log 2, log 4, log 8, log 16, . . . an arithmetic sequence?
Solve the problem.Suppose that a1, a2, a3, a4, a5, . . . is an arithmetic sequence. Is a1, a3, a5, . . . an arithmetic sequence?
Solve the problem.The normal growth pattern for children aged 3–11 follows that of an arithmetic sequence. An increase in height of about 6 cm per year is expected. Thus, 6 would be the common difference of the sequence. For example, a child who measures 96 cm at age 3 would have his
Solve each problem.How much material will be needed for the rungs of a ladder of 31 rungs, if the rungs taper uniformly from 18 in. to 28 in.?
Solve the problem.A super slide of uniform slope is to be built on a level piece of land. There are to be 20 equally spaced vertical supports, with the longest support 15 m long and the shortest 2 m long. Find the total length of all the supports.
Write a formula for the nth term of the finite arithmetic sequence an shown in each graph. Then state the domain and range of the sequence. 15 10 п -5
Match each equation of a hyperbola in Column I with its description in Column II. (y – 1)2 (x – 2)? 25
Use the following matrices, where all elements are real numbers, to show that each statement is true for 2 × 2 matrices.(cd)A = c(dA), for any real numbers c and d. с сд) аи ан] b11 b12 [b21 b2] C11 C12 [C21 C22 a11 a12 A = [a21 a2. and C= B =
Use the following matrices, where all elements are real numbers, to show that each statement is true for 2 × 2 matrices.c(A)d = (cd)A, for any real numbers c and d. с сд) аи ан] b11 b12 [b21 b2] C11 C12 [C21 C22 a11 a12 A = [a21 a2. and C= B =
Use the following matrices, where all elements are real numbers, to show that each statement is true for 2 × 2 matrices.(c + d)A = cA + dA, for any real numbers c and d. с сд) аи ан] b11 b12 [b21 b2] C11 C12 [C21 C22 a11 a12 A = [a21 a2. and C= B =
Use the following matrices, where all elements are real numbers, to show that each statement is true for 2 × 2 matrices.c(A + B) = cA + cB, for any real number c. с сд) аи ан] b11 b12 [b21 b2] C11 C12 [C21 C22 a11 a12 A = [a21 a2. and C= B =
Use the following matrices, where all elements are real numbers, to show that each statement is true for 2 × 2 matrices.A(B + C) = AB + AC (distributive property) с сд) аи ан] b11 b12 [b21 b2] C11 C12 [C21 C22 a11 a12 A = [a21 a2. and C= B =
Use the following matrices, where all elements are real numbers, to show that each statement is true for 2 × 2 matrices.(AB)C = A(BC) (associative property) с сд) аи ан] b11 b12 [b21 b2] C11 C12 [C21 C22 a11 a12 A = [a21 a2. and C= B =
Use the following matrices, where all elements are real numbers, to show that each statement is true for 2 × 2 matrices.A + (B + C) = (A + B) + C (associative property) с сд) аи ан] b11 b12 [b21 b2] C11 C12 [C21 C22 a11 a12 A = [a21 a2. and C= B =
Use the following matrices, where all elements are real numbers, to show that each statement is true for 2 × 2 matrices.A + B = B + A (commutative property) с сд) аи ан] b11 b12 [b21 b2] C11 C12 [C21 C22 a11 a12 A = [a21 a2. and C= B =
Solve the equation. х |2 -3 = 12 х х 7,
Solve the equation. 2x 1 %3| 3 0 2
Solve the equation. Зх —3 = -7 2 -1 4 -1 х
Solve the equation. 4 3 2 0 = 5 —3 х -1 ||
Solve the equation. Give solutions in exact form. In x – 4 In 3 = In-x
Solve the equation. Give solutions in exact form.log2 x + log2 (x + 2) = 3
Solve each equation. Give solutions in exact form.log2 [(x - 4)(x - 2)] = 3
Solve each equation. Give solutions in exact form. log, = 2 16
Solve each equation. Give irrational solutions as decimals correct to the nearest thousandth.2e2x - 5ex + 3 = 0 (Give both exact and approximate values.)
Solve each equation. Give irrational solutions as decimals correct to the nearest thousandth.e0.4x = 4x-2
Solve each equation. Give irrational solutions as decimals correct to the nearest thousandth.2x+1 = 3x-4
Solve each equation. Give irrational solutions as decimals correct to the nearest thousandth.162x+1 = 83x
Solve each equation. Give irrational solutions as decimals correct to the nearest thousandth.9x = 4
Solve each equation. Give irrational solutions as decimals correct to the nearest thousandth.12x = 1
Use a calculator to find an approximation to four decimal places for each logarithm.Solve x2/3 = 25.
Use a calculator to find an approximation to four decimal places for each logarithm.log9 13
Use a calculator to find an approximation to four decimal places for each logarithm.ln 2388
Use a calculator to find an approximation to four decimal places for each logarithm.log 2388
Use properties of logarithms to rewrite the expression. Assume all variables represent positive real numbers. x²V 'y log7
Graph ƒ(x) = (1/2)x and g(x) = log1/2 x on the same axes. What is their relationship?
(a) Write 43/2 = 8 in logarithmic form.(b) Write log8 4 = 2/3 in exponential form.
Solve 2x-3 = 16*+1. 8.
Match each equation with its graph. х (b) y = e* (d) y = (a) y = log13 x (c) y = In x B. C. D. A. х х
Then solve to obtain the solution set {-1}. Use this method to solve each equation. -2 3 = 3 5 -2 0
Then solve to obtain the solution set {-1}. Use this method to solve each equation. 2х х |11 х
Showing 10600 - 10700
of 16373
First
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
Last
Step by Step Answers
Get 50% OFF
Claim Now
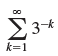
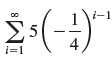
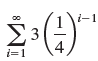
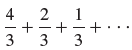
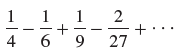
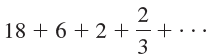
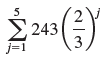
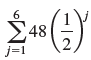
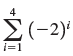
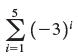
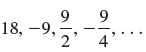
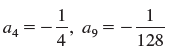
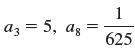
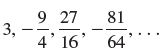
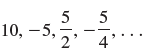
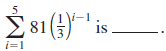
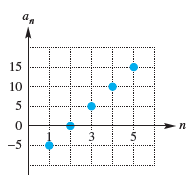
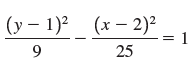
![с сд) аи ан] b11 b12 [b21 b2] C11 C12 [C21 C22 a11 a12 A = [a21 a2. and C= B =](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1555/1/4/7/5735cb1ab3584b8b1555130396235.jpg)
