Let \(S_{0} \subset \mathbb{R}^{2}\) be a solid equilateral triangle. We get \(S_{1}\) by removing the middle triangle whose vertices are the midpoints of the sides of \(S_{1}\). By repeating this procedure with the four triangles which make up \(S_{1}\) etc. we get \(S_{0}, S_{2}, S_{2}, \ldots\) (see Fig. 1.6 ). The Sierpiński triangle is \(S_{\infty}:=\bigcap_{n=0}^{\infty} S_{n}\). Find the area of \(S_{n}\) and \(S\) if the side-length of \(S_{0}\) is \(s=1\).

Figure 1.6

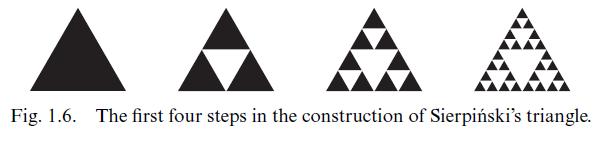
Fig. 1.6. The first four steps in the construction of Sierpiski's triangle.