Monotone classes (1). A family \(\mathscr{M} \subset \mathscr{P}(X)\) which contains \(X\) and is stable under countable unions of increasing sets and countable intersections of decreasing sets.

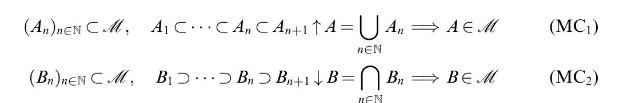
is called a monotone class. Assume that \(\mathscr{M}\) is a monotone class and \(\mathscr{F} \subset \mathscr{P}(X)\) any family of sets.

(i). Mimic the proof of Theorem 3.4 to show that there is a minimal monotone class \(\mathfrak{m}(\mathscr{F})\) such that \(\mathscr{F} \subset \mathfrak{m}(\mathscr{F})\).

(ii). If \(\mathscr{F}\) is stable w.r.t. complements, i.e. \(F \in \mathscr{F} \Longrightarrow F^{c} \in \mathscr{F}\), then so is \(\mathfrak{m}(\mathscr{F})\).

(iii). If \(\mathscr{F}\) is \(\cap\)-stable, i.e. \(F, G \in \mathscr{F} \Longrightarrow F \cap G \in \mathscr{F}\), then so is \(\mathfrak{m}(\mathscr{F})\).

[ show that the families]

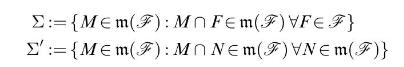
are again monotone classes satisfying \(\mathscr{F} \subset \Sigma, \Sigma^{\prime}\).]

(iv). Use (i)-(iii) to prove the following.

Monotone class theorem. Let \(\mathscr{F} \subset \mathscr{P}(X)\) be a family of sets which is stable under the formation of complements and intersections. If \(\mathscr{M} \supset \mathscr{F}\) is a monotone class, then \(\mathscr{M} \supset \sigma(\mathscr{F})\).

Data from theorem 3.4

Transcribed Image Text:

(An)EN CM, AC... CA C An+11A=U An A M (Bn)neNCM, B B B+1+B= B BEM. = #EN "EN (MC) (MC)