Consider the eigenvalue problem: where Equation (E.1) can be expressed as [[D] vec{X}=lambda vec{X}] where [[D]=left([m]^{frac{1}{2}} ight)^{-1}[k]left([m]^{frac{1}{2}} ight)^{-1}] is called the mass normalized stiffness matrix.

Consider the eigenvalue problem:

where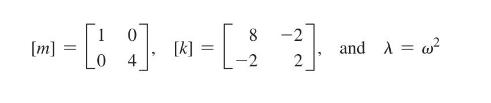 

Equation (E.1) can be expressed as

\[[D] \vec{X}=\lambda \vec{X}\]

where

\[[D]=\left([m]^{\frac{1}{2}}\right)^{-1}[k]\left([m]^{\frac{1}{2}}\right)^{-1}\]

is called the mass normalized stiffness matrix. Determine the mass normalized stiffness matrix and use it to find the eigenvalues and orthonormal eigenvectors of the problem stated in Eq. (E.1).
The square root of a diagonal matrix \([\mathrm{m}]\), of order \(n\), is given by 

A[m]X = [k]X (E.1)