Linearize the governing equations of Problem 3 shown below and find the natural frequencies and mode shapes for \(m_{1}=m_{2}=m\) and \(l_{1}=l_{2}=l\). State all assumptions in the linearization process:

\[ \begin{aligned} & \left(m_{1}+m_{2}\right) l_{1} \ddot{\theta}_{1}+m_{2} l_{2}\left[\ddot{\theta}_{2} \cos \left(\theta_{2}-\theta_{1}\right)\right. \\ & \left.-\dot{\theta}_{2}^{2} \sin \left(\theta_{2}-\theta_{1}\right)\right]+\left(m_{1}+m_{2}\right) g \sin \theta_{1}=0 \\ & \quad m_{2} l_{2} \ddot{\theta}_{2}+m_{2} l_{1}\left[\ddot{\theta}_{1} \cos \left(\theta_{2}-\theta_{1}\right)\right. \\ & \left.\quad+\dot{\theta}_{1}^{2} \sin \left(\theta_{2}-\theta_{1}\right)\right]+m_{2} g \sin \theta_{2}=0 \end{aligned} \]

Problem 3:

For the double pendulum of Figure 6.66, derive the equations of motion using

(a) Newton's second law, and

(b) Lagrange's equation.

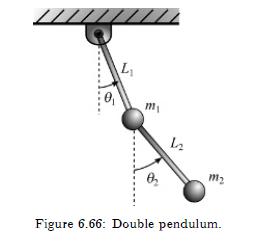
L 0 m m Figure 6.66: Double pendulum.