Show that the shape (r(varphi)) for a central spring force ellipse takes the standard form (r^{2}=a^{2} b^{2} /left(b^{2} cos ^{2} varphi+a^{2} sin ^{2} varphi ight))

Show that the shape \(r(\varphi)\) for a central spring force ellipse takes the standard form \(r^{2}=a^{2} b^{2} /\left(b^{2} \cos ^{2} \varphi+a^{2} \sin ^{2} \varphi\right)\) if (in equation 7.37) we use the plus sign in the denominator and choose \(\varphi_{0}=\pi / 4\).

Data from equation 7.37

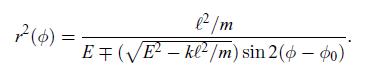
7(6) = Im EVE-kl/m) sin 2(0-0)