Question: (a) Consider a collection of photons with a distribution function N that, in the mean rest frame of the photons, is isotropic. Show, using Eqs.
(a) Consider a collection of photons with a distribution function N that, in the mean rest frame of the photons, is isotropic. Show, using Eqs. (3.49b) and (3.49c), that this photon gas obeys the equation of state P = 1/3ρ.
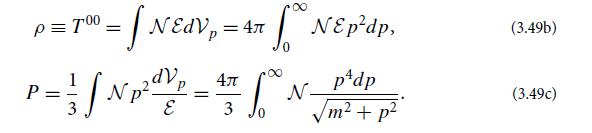(b) Suppose the photons are thermalized with zero chemical potential (i.e., they are isotropic with a blackbody spectrum). Show that ρ =aT4, where a is the radiation constant of Eq. (3.54c).
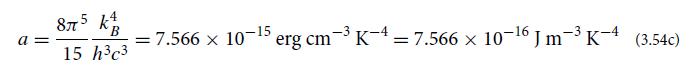(c) Show that for this isotropic, blackbody photon gas the number density of photons is n = bT3, where b is given by Eq. (3.54b), and that the mean energy of a photon in the gas is
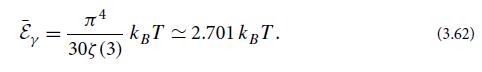
00 = [ NEDV = 4x * NEpdp, P = 700 4 = = N200 = 47 N- P 3 pdp m + p (3.49b) (3.49c)
Step by Step Solution
3.34 Rating (160 Votes )
There are 3 Steps involved in it
a To show that the photon gas obeys the equation of state P 13 well use the equations 349b and 349c given P T00 N First lets calculate T00 T00 NEvdp 47 NEp dp Np2 3 Npdp m p Now we can calculate NEp d... View full answer
Get step-by-step solutions from verified subject matter experts
Study Help