Consider a collection of identical, classical (i.e., with 1) particles with a distribution function N that is thermalized at a temperature T such

Consider a collection of identical, classical (i.e., with η ≪ 1) particles with a distribution function N that is thermalized at a temperature T such that k_BT ≪ mc² (nonrelativistic temperature).(a) Show that the distribution function, expressed in terms of the particles’ momenta or velocities in their mean rest frame, is

with v being the speed of a particle.

(b) Show that the number density of particles in the mean rest frame is given by Eq. (3.39a).

(c) Show that this gas satisfies the equations of state (3.39b).

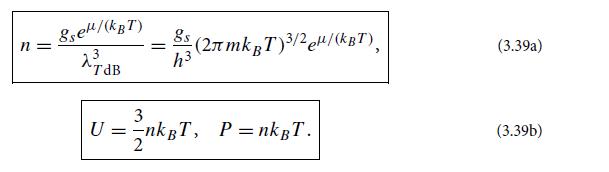
N = 8se/(KBT) e-p/(2mk BT), where p where p = [p] = mv, h3 (3.56)