(a) Near the event {r = 2M, = o , = o , t finite}, on the horizon of a black

(a) Near the event {r = 2M, θ = θ_o, ∅ = ∅_o, t finite}, on the horizon of a black hole, introduce locally Cartesian spatial coordinates

accurate to first order in distance from that event. Show that the metric in these coordinates has the form(accurate to leading order in distance from the chosen event):

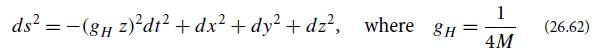
is the horizon’s so-called surface gravity, to which we shall return, for a rotating black hole, in Eq. (26.90).

(b) Notice that the metric (26.62) is the same as that for flat spacetime as seen by a family of uniformly accelerated observers. Why is this physically reasonable?

Equation 26.90.

{x = 2M sin 0,(Po), y = 2M (0 - 0), z = = SM dr/1-2M/r},