(a) Show that, as the surface of an imploding star approaches R = 0, its world line in Schwarzschild coordinates asymptotes to the curve {(t , θ , ∅) = const, r variable}.

(b) Show that this curve to which it asymptotes [part (a)] is a timelike geodesic.

(c) Show that the basis vectors of the infalling observer’s local Lorentz frame near r = 0 are related to the Schwarzschild coordinate basis by

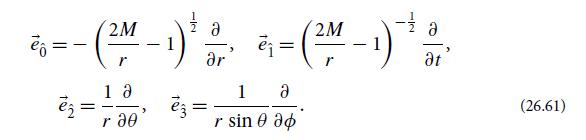
What are the components of the Riemann tensor in that local Lorentz frame?

(d) Show that the tidal forces produced by the Riemann tensor stretch an infalling observer in the radial, e_1̂(vector), direction and squeeze the observer in the tangential, e_2̂(vector) and e_3̂(vector), directions. Show that the stretching and squeezing forces become infinitely strong as the observer approaches r = 0.

(e) Idealize the body of an infalling observer to consist of a head of mass μ ≈ 20 kg and feet of mass μ ≈ 20 kg separated by a distance h ≈ 2m, as measured in the observer’s local Lorentz frame, and with the separation direction radial. Compute the stretching force between head and feet, as a function of proper time τ, as the observer falls into the singularity. Assume that the hole has the mass M = 7 × 10⁹M_⊙, which has been measured by astronomical observations for the black hole at the center of the supergiant elliptical galaxy M87. How long before hitting the singularity (at what proper time τ) does the observer die, if he or she is a human being made of flesh, bone, and blood?

2 2 % = 1 --(M_) 1.4= (2M -1)+ a - r ar r t 18 1 r sin 0 = > - (26.61)