Consider a classical, nonrelativistic gas whose particles do not interact and have no excited internal degrees of freedom (a perfect gas—not to be confused with perfect fluid). Let the gas be contained in a volume V and be thermalized at temperature T and chemical potential μ. Using the gas’s entropy per mode, Ex. 4.4, show that the total entropy in the volume V is

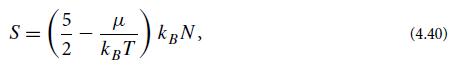
where N = g_s(2πmk_BT/h²)^3/2e^μ/(kBT)V is the number of particles in the volume V and g_s is each particle’s number of spin states

Data from Ex 4.4

Consider a mode S of a fermionic or bosonic field. Suppose that an ensemble of identical such modes is in statistical equilibrium with a heat and particle bath and thus is grand canonically distributed.

(a) Show that if S is fermionic, then the ensemble’s entropy is

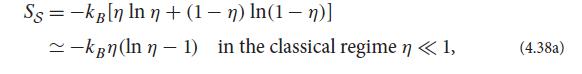
where η is the mode’s fermionic mean occupation number (4.27b).

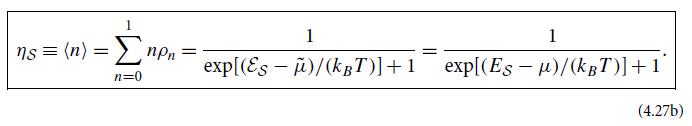
(b) Show that if the mode is bosonic, then the entropy is

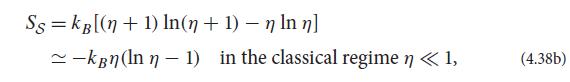
where η is the bosonic mean occupation number (4.28b). Note that in the classical regime,

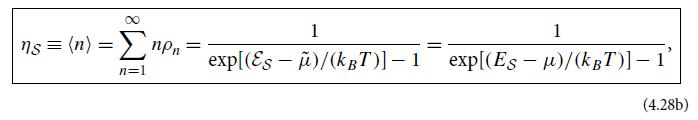
the entropy is insensitive to whether the mode is bosonic or fermionic.

(c) Explain why the entropy per particle in units of Boltzmann’s constant is σ = S_S/(ηk_B). Plot σ as a function of η for fermions and for bosons. Show analytically that for degenerate fermions (η ≈ 1) and for the bosons’ classical-wave regime (η >> 1) the entropy per particle is small compared to unity.

5 S= (2-LT) KBN, B (4.40)