Consider a mode S of a fermionic or bosonic field. Suppose that an ensemble of identical such modes is in statistical equilibrium with a heat and particle bath and thus is grand canonically distributed.

(a) Show that if S is fermionic, then the ensemble’s entropy is

where η is the mode’s fermionic mean occupation number (4.27b).

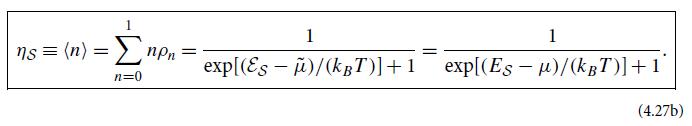
(b) Show that if the mode is bosonic, then the entropy is

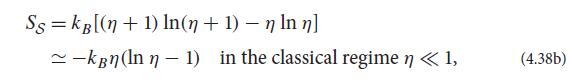
where η is the bosonic mean occupation number (4.28b). Note that in the classical regime,

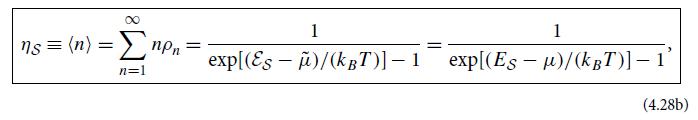
the entropy is insensitive to whether the mode is bosonic or fermionic.

(c) Explain why the entropy per particle in units of Boltzmann’s constant is σ = S_S/(ηk_B). Plot σ as a function of η for fermions and for bosons. Show analytically that for degenerate fermions (η ≈ 1) and for the bosons’ classical-wave regime (η >> 1) the entropy per particle is small compared to unity.

Ss-kB [n Inn + (1 n) ln(1 n)] ~-ken (In n-1) in the classical regime n < < 1, (4.38a)