Consider hydrogen gas in statistical equilibrium at a temperature T ec²/kB ≈ 6 × 10⁹ K. Electrons at the high-energy end of the Boltzmann energy distribution can produce electron-positron pairs by scattering off protons:

(a) In statistical equilibrium, the reaction (5.65) and its inverse must proceed on average at the same rate. What does this imply about the relative magnitudes of the electron and positron chemical potentials μ̃− and μ̃+ (with rest masses included)?

(b) Although these reactions require an e⁻ that is relativistic in energy, almost all the electrons and positrons will have kinetic energies of magnitude 

and thus they will have 

What are the densities in phase space N_± = dN_±/(d³xd³p) for the positrons and electrons in terms of p, μ̃±, and T ? Explain why for a hydrogen gas we must have μ̃₋ > 0 and μ̃₊

(c) Assume that the gas is very dilute, so that η

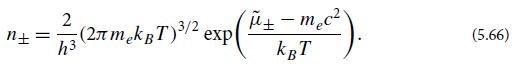
In cgs units, what does the dilute-gas assumption η ±?What region of hydrogen mass density ρ and temperature T is the dilute-gas region?

(d) Let n be the number density of protons. Then by charge neutrality, n = n₋ − n₊ will also be the number density of “ionization electrons” (i.e., of electrons that have been ionized off of hydrogen). Show that the ratio of positrons (and hence of pairs) to ionization electrons is given by

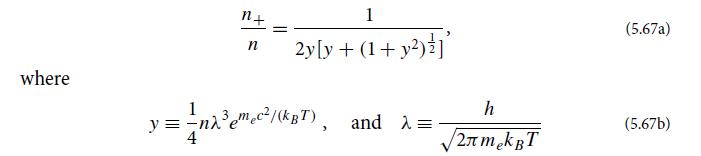
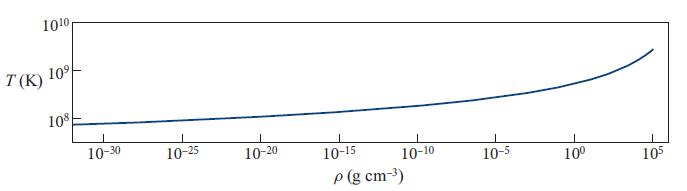
is the thermal deBroglie wavelength of the electrons. Figure 5.7 shows the temperature T_p at which, according to this formula, n₊ = n (and y = 0.354), as a function of mass density ρ ≈ m_protonn. This T_p can be thought of as the temperature at which pairs form in a dilute plasma. Somewhat below T_p there are hardly any pairs; somewhat above, the pairs are profuse.

(e) Note that at low densities pairs form at temperatures T ∼ 10⁸ K ≈ 0.02m_ec²/k_B. Explain qualitatively in terms of available phase space why the formation temperature is so low.

Fig 5.7.

Transcribed Image Text:

e+pe+p+e¯¯ +e+. (5.65)