Consider small-amplitude (linear) shallow-water waves in which the height of the bottom boundary varies, so the unperturbed water’s depth is variable: h_o = h_o(x, y).

(a) Using the theory of nonlinear shallow-water waves with variable depth (Box 16.3), show that the wave equation for the perturbation ξ(x, y, t) of the water’s height takes the form

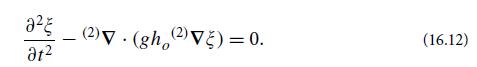
Here ⁽²⁾∇ is the 2-dimensional gradient operator that acts in the horizontal (i.e., x-y) plane. Note that gh_o is the square of the wave’s propagation speed C² (phase speed and group speed), so this equation takes the same form as Eq. (7.17) from the geometric-optics approximation in Sec. 7.3.1, with W = 1.

(b) Describe what happens to the direction of propagation of a wave as the depth h_o of the water varies (either as a set of discrete jumps in h_o or as a slowly varying h_o). As a specific example, how must the propagation direction change as waves approach a beach (but when they are sufficiently far out from the beach that nonlinearities have not yet caused them to begin to break)? Compare with your own observations at a beach.

(c) Tsunamis are gravity waves with enormous wavelengths (∼100 km or so) that propagate on the deep ocean. Since the ocean depth is typically h_o ∼ 4 km, tsunamis are governed by the shallow-water wave equation (16.12).What would you have todo to the ocean floor to create a lens that would focus a tsunami, generated
by an earthquake near Japan, so that it destroys LosAngeles? (For simulations of tsunami propagation, see, e.g., http://bullard.esc.cam.ac.uk/~taylor/Tsunami.html.)

(d) The height of a tsunami, when it is in the ocean with depth h_o ∼ 4 km, is only ∼1m or less. Use the geometric-optics approximation (Sec. 7.3) to show that the tsunami’s wavelength decreases as λ ∝ √h_o and its amplitude increases as max(ξ ) ∝ 1/h_o^1/4 as the tsunami nears land and the water’s depth ho decreases. How high [max(ξ )] does the tsunami get when nonlinearities become strongly important? (Assume a height of 1 m in the deep ocean.)How does this compare with the heights of historically disastrous tsunamis when they hit land? From your answer you should conclude that the nonlinearities must play a major role in raising the height. Equations (16.11) in Box 16.3 are used by geophysicists to analyze this nonlinear growth of the tsunami height. If the wave breaks, then these equations fail, and ideas developed (in rudimentary form) in Ex. 17.10 must be used.

Equation 17.17.

Data from Exercises 17.10.

Run water at a high flow rate from a kitchen faucet onto a dinner plate (Fig. 17.12). What you see is called a hydraulic jump. It is the kitchen analog of a breaking ocean wave, and the shallow-water-wave analog of a shock front in a compressible gas. In this exercise you will develop the theory of hydraulic jumps (and breaking ocean waves) using the same tools as those used for shock fronts.

(a) Recall that for shallow-water waves, the water motion, below the water’s surface, is nearly horizontal, with speed independent of depth z (Ex. 16.1). The same is true of the water in front of and behind a hydraulic jump. Apply the conservation of mass and momentum to a hydraulic jump, in the jump’s rest frame, to obtain equations for the height of the water h₂ and water speed v₂ behind the jump (emerging from it) in terms of those in front of the jump, h₁ and v₁. These are the analog of the Rankine-Hugoniot relations for a shock front.

(b) You did not use energy conservation across the jump in your derivation, but it was needed in the analysis of a shock front. Why?

(c) Show that the upstream speed v₁ is greater than the speed √gh₁ of small amplitude, upstream gravity waves [shallow-water waves; Eq. (16.10) and associated discussion]; thus the upstream flow is supersonic. Similarly, show that the downstream flow speed v₂ is slower than the speed √gh₂ of small-amplitude, downstream gravity waves (i.e., the downstream flow is subsonic).

(d) We normally view a breaking ocean wave in the rest frame of the quiescent upstream water. Use your hydraulic-jump equations to show that the speed of the breaking wave as seen in this frame is related to the depths h₁ and h₂ in front of and behind the breaking wave by

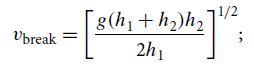
Figure 17.12

Transcribed Image Text:

22 812 . (2)V · (gho(2)VĚ) = 0. (16.12)