By a method analogous to that used for the elementary fluctuation-dissipation theorem, derive the generalized fluctuation-dissipation theorem [Eqs. (6.86)].

Consider a thought experiment in which the system’s generalized coordinate q is very weakly coupled to an external oscillator that has a mass M and an angular eigenfrequency ω_o, near which we wish to derive the fluctuation-dissipation formulas (6.86). Denote by Q and P the external oscillator’s generalized coordinate and momentum and by κ the arbitrarily weak coupling constant between the oscillator and q, so the hamiltonian of system plus oscillator plus fluctuating force F' acting on q is

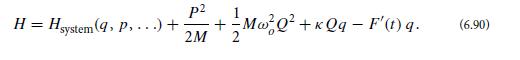
Here the “. . .” refers to the other degrees of freedom of the system, some of which might be strongly coupled to q and p.

(a) By combining Hamilton’s equations for q and its conjugate momentum p [which give Eq. (6.83a) with the appropriate driving force] with those for the external oscillator (Q, P), derive an equation that shows quantitatively how the force F', acting through q, influences the oscillator’s coordinate Q:

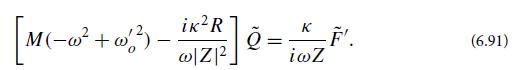
Here the tildes denote Fourier transforms; ω = 2πf is the angular frequency at which the Fourier transforms are evaluated; and

with Z = R + iI , is the impedance of q at angular frequency ω.

(b) Show that

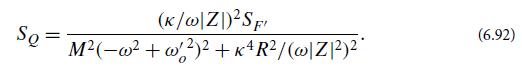
(c) Make the resonance in this equation arbitrarily sharp by choosing the coupling constant κ arbitrarily small. Then show that the mean energy in the oscillator is

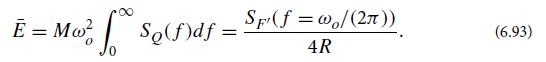
(d) By equating this to expression (6.75c) for the mean energy of any oscillator coupled to a heat bath, deduce the desired generalized fluctuation-dissipation equations (6.86).

Equations.

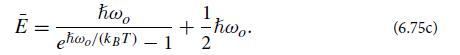
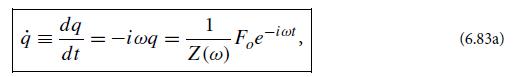
p H = Hsystem (9, P,...) + PM +MwQ + xQq - F' (1) q. 2M (6.90)