In this exercise we explore nonlinear effects in ion-acoustic waves (Ex. 21.5), and show that they give rise to solitons that obey the same KdV equation as governs solitonic water waves. This version of the solitons is only mildly nonlinear. In Sec. 23.6 we will generalize to strong nonlinearity.

(a) Introduce a bookkeeping expansion parameter ε whose numerical value is unity,⁵ and expand the ion density, ion velocity, and potential in the forms

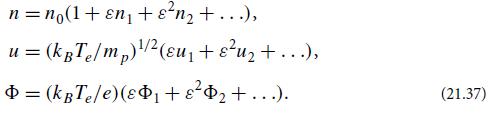
Here n₁, u₁, and Φ₁ are small compared to unity, and the factors of ε tell us that, as the wave amplitude is decreased, these quantities scale proportionally to one another, while n₂, u₂, and Φ₂ scale proportionally to the squares of n₁, u₁, and Φ₁, respectively. Change independent variables from (t , z) to (τ , η), where

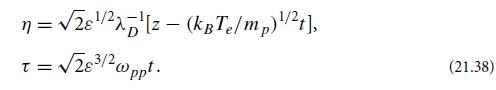
Explain, now or at the end, the chosen powers ε^1/2 and ε^3/2. By substituting Eqs. (21.37) and (21.38) into the nonlinear equations (21.35), equating terms of the same order in ε, and then setting ε = 1 (bookkeeping parameter!), show that n₁, u₁, and Φ₁ each satisfy the KdV equation (16.32):

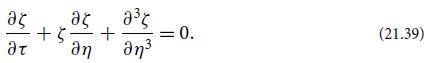
(b) In Sec. 16.3 we discussed the exact, single-soliton solution (16.33) to this KdV equation. Show that for an ion-acoustic soliton, this solution propagates with the physical speed (1+ n_1o)(k_BT_e/m_p)^1/2 (where n_1o is the value of n₁ at the peak of the soliton), which is greater the larger is the wave’s amplitude.

Equations.

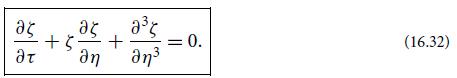
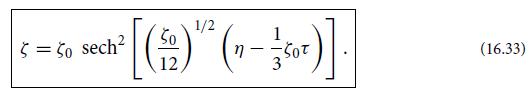
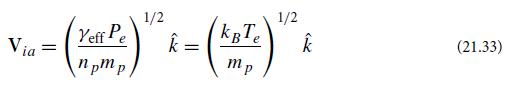
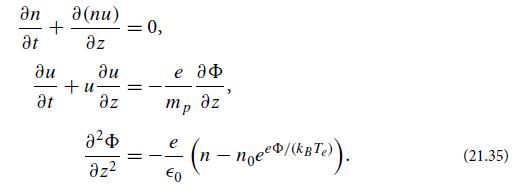
Data from Exercises 21.5.

Ion-acoustic waves can propagate in an unmagnetized plasma when the electron temperature T_e greatly exceeds the ion temperature T_p. In this limit, the electron density n_e can be approximated by n_e = n₀ exp[eΦ/(k_BT_e)], where n₀ is the mean electron density, and Φ is the electrostatic potential.

(a) Show that for ion-acoustic waves that propagate in the z direction, the nonlinear equations of continuity, the motion for the ion (proton) fluid, and Poisson’s equation for the potential take the form

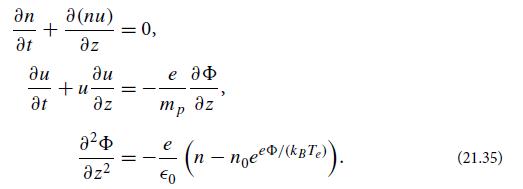
Here n is the proton density, and u is the proton fluid velocity (which points in the z direction).

(b) Linearize Eqs. (21.35), and show that the dispersion relation for small-amplitude ion-acoustic modes is

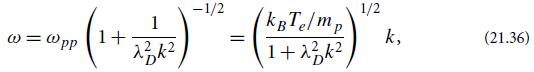
where λ_D is the Debye length.

n=no(1+ n +8m + ...), = (ke/mp)/(u + + ), u= = (kBT/e) ( + 8 + ...). (21.37)