To measure a very weak sinusoidal force, let the force act on a simple harmonic oscillator with eigenfrequency at or near the force’s frequency, and measure the oscillator’s response. Examples range in physical scale from nanomechanical oscillators (∼1μm in size) with eigenfrequency ∼1GHz that might play a role in future quantum information technology (e.g., Chan et al., 2011), to the fundamental mode of a ∼10-kg sapphire crystal, to a∼40-kg LIGO mirror on which light pressure produces a restoring force, so its center of mass oscillates mechanically at frequency ∼100 Hz (e.g., Abbott et al., 2009a). The oscillator need not be mechanical; for example, it could be an L-C-R circuit, or a mode of an optical (Fabry-Perot) cavity. The displacement x(t) of any such oscillator is governed by the driven-harmonic oscillator equation

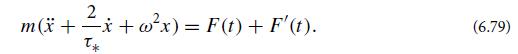
Herem, ω, and τ_∗ are respectively the effective mass, angular frequency, and amplitude damping time associated with the oscillator; F(t) is an external driving force; and F'(t) is the fluctuating force associated with the dissipation that gives rise to τ_∗. Assume that ωτ_∗>> 1 (weak damping).

(a) Weak coupling to other modes is responsible for the damping. If the other modes are thermalized at temperature T , what is the spectral density S_F'(f) of the fluctuating force F´? What is the spectral density S_x(f ) of x?

(b) A very weak sinusoidal force drives the fundamental mode precisely on resonance:

Here F_s is the rms signal. What is the x(t) produced by this signal force?

(c) A sensor with negligible noise monitors this x(t) and feeds it through a narrowband filter with central frequency f = ω/(2π) and bandwidth △f = 1/ˆτ (whereˆτ is the averaging time used by the filter). Assume that ˆτ >> τ∗. What is the rms thermal noise σ_x after filtering? Show that the strength F_s of the signal force that produces a signal x(t) =  √2x_s cos(ωt + δ) with rms amplitude x_s equal to σ_x and phase δ is

This is the minimum detectable force at the “one-σ level.”

(d) Suppose that the force acts at a frequency ω_o that differs from the oscillator’s eigenfrequency ω by an amount

What, then, is the minimum detectable force strength F_s? What might be the advantages and disadvantages of operating off resonance in this way, versus on resonance?

m(x + x+wx) = F(t) + F'(t). (6.79)