Using the method introduced in Question 24, find the solutions of the following initial-value problems:

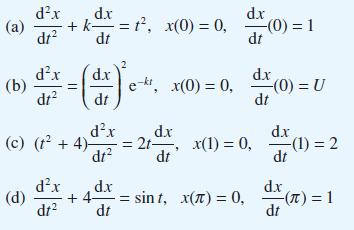
Data from Question 24

Show that by making the substitution

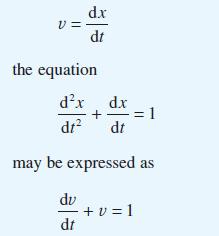
Show that the solution of this equation is v = 1 + Ce^–t and hence find x(t). This technique is a standard method for solving second-order differential equations in which the dependent variable itself does not appear explicitly. Apply the same method to obtain the solutions of the differential equations

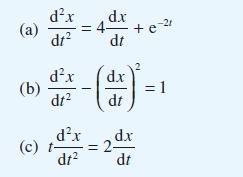
dx (a) + k- dr (b) dx dt (d) (c) (t + 4) dx dt d.x dt dx dt dx dr = t, x(0) = 0, e-kt, x(0) = 0, dx dt - + 4x = sint, x() = 0, dt dx 2t, x(1) = 0, dt -(0)=1 dx -(0) = U dt dx dt d.x (1)=2 -(T) = 1 dt