Show that by making the substitution

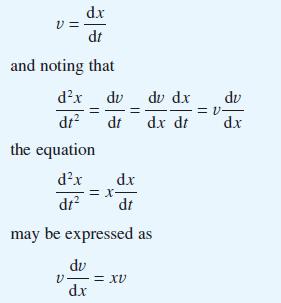
Show that the solution of this equation is v = 1/2x² + C and hence find x(t). This technique is a standard method for solving second-order differential equations in which the independent variable does not appear explicitly. Apply the same method to obtain the solutions of the differential equations

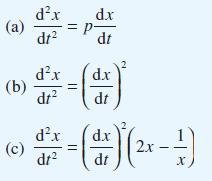
d.x dt and noting that dx du dt dt the equation dx dt may be expressed as v= du dx d.x -X = || ax=a dt du dx dx dt du dx = V-