The signed-rank statistic can be represented as S₊ = 1 · U₁ + 2 · U₂+.....+ n · U_n where U_i = 1 if the sign of the (x_i − µ₀) with the ith largest absolute magnitude is positive (in which case i is included in S₊) and U_i = 0 if his value is negative (i = 1, 2, 3, …, n). Furthermore, when H₀ is true, the U_i’s are independent Bernoulli rvs with p = .5. 

a. Use this representation to obtain the mean and variance of S₊ when H₀ is true. The sum of the first n positive integers is n(n + 1) / 2, and the sum of the squares of the first n positive integers is n(n + 1)(2n + 1) = 6.

b. A particular type of steel beam has been designed to have a compressive strength (lb/in²) of at least 50,000. An experimenter obtained a random sample of 25 beams and determined the strength of each one, resulting in the following data (expressed as deviations from 50,000):

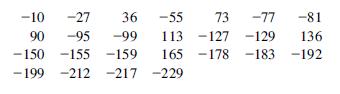
Carry out a test using a significance level of approximately .01 to see if there is strong evidence that the design condition has been violated.

-10 -27 36 -55 73 -77 -81 90 -95 -99 113 -127-129 136 -150 -155 -159 165 -178 -183 -192 -199 -212 -217-229