Prove Eq. (15.28) for lightlike particles. Use Eq. (15.26) for the standard vector and take note of the Minkowski metric, so \(p_{\mu}=\eta_{\mu u} p^{v}\) and \(L^{\mu u}=\eta^{\mu \lambda} L_{\lambda \sigma} \eta^{\sigma v}\). You also will need Eq. (15.27) and results of Problem 15.8 .

Data from Problem 15.8

Use Eq. (15.10) to prove that \(J_{1}=L_{23}, J_{2}=L_{31}\), and \(J_{3}=L_{12}\).

Data from Eq. 15.26

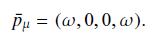
Data from Eq. 15.27

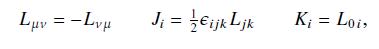
Data from Eq. 15.28

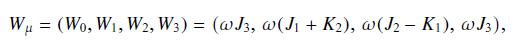
= Pu(w, 0, 0, w).