Question: Show that for a four-dimensional cartesian space ((x, y, z, t)) the operators which is the algebra associated with the group (mathrm{SO}(4)). Show that this

Show that for a four-dimensional cartesian space \((x, y, z, t)\) the operators

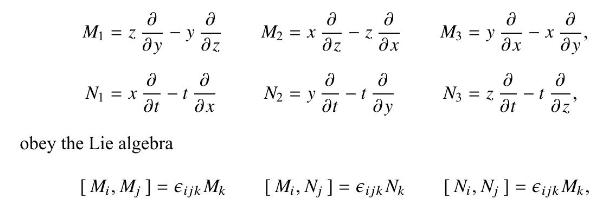
M = z a a a y M = x - M3

which is the algebra associated with the group \(\mathrm{SO}(4)\). Show that this \(\mathrm{SO}(4)\) is locally isomorphic to \(\mathrm{SU}(2) \times \mathrm{SU}(2)\) by showing that the new operator set,

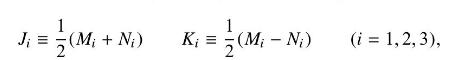
= y x z z a N = y - 1 a

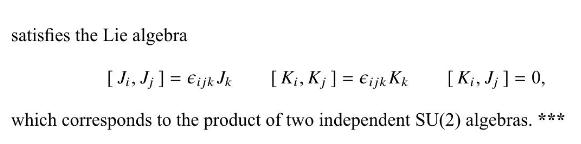
- N3 = 2 - - t N = X a -

M = z a a a y M = x - M3 = y x z z a N = y - 1 a - N3 = 2 - - t N = X a - - obey the Lie algebra [Mi, M;] Eijk Mk [Mi, Nj] = ijk Nk [Ni, Nj] = Eijk Mk,

Step by Step Solution

★★★★★

3.33 Rating (159 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The commutat... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Physics Questions!

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

answer the question clearly You are building a flight-control system for which a convincing safety case must be made. Would you assign the tasks of safety requirements engineering, test case...

Using the commutators for \(J_{i}\) and \(K_{i}\) given in Problem 3.8 , argue that the \(\mathrm{SO}(4)\) Lie algebra is semisimple, but not simple. Argue that \(\mathrm{SO}(4)\) can be written as a...

Microkernel operating systems aim to address perceived modularity and reliability issues in traditional "monolithic" operating systems. (i) Describe the typical architecture of a microkernel...

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

Let r and s be solutions to the quadratic equation x 2 b x + c = 0. For n N, define d0 = 0 d1 = r s dn = b dn1 c dn2 (n 2) Prove that dn = r n s n for all n N. [4 marks] (b) Recall that a commutative...

Satellite Data Retrieval, Reference Frames, Numerical and Analytical Orbital Propagation SSD Individual Assignment RMIT University Figure 1: Example errors between a ground truth ephemeris and...

(i) Write down the linear program relaxation for the vertex cover problem and solve the linear program. [6 marks] (ii) Based on the solution of the linear program in (b)(i), derive an integer...

nnep This counts as "setting the value", even if the value does not change. If its value was last set to v 6= n less than 30 seconds ago, it leaves its value unchanged and replies false. If a client...

Single Audit, Internet Case. A not-for-profit organization has hired you to conduct an audit. The audit has been requested by the organizations board of directors. A mission of the organization is to...

Suppose that a point (X, Y) is to be chosen at random in the xy-plane, where X and Y are independent random variables and each has the standard normal distribution. If a circle is drawn in the...

29. What is a Summary of Significant Accounting Policies?

Based on the following information, how many components should be extracted, using (a) the eigenvalue criterion and (b) the proportion of variance explained criterion? Initial Eigenvalues Component...

In no more than three PowerPoint slides, list some general guidelines that a taxpayer can use to determine whether it has an obligation to file an income tax return with a particular state. (Include...

Fallow Corporation is subject to tax only in State X. Fallow generated the following income and deductions. State income taxes are not deductible for X income tax purposes. Sales...

Dillman Corporation has nexus in States A and B. Dillmans activities for the year are summarized below. Determine the apportionment factors for A and B assuming that A uses a three-factor...

please use the excel functions PMT- Calculates the payment of a loan with the assumption that the rate and payment amount does not change. PV. Calculates the present or current value of an...

Vaughn Company follows the practice of pricing its inventory at the lower-of-cost-or-market, item basis. on an individual- Item Cost per Cost to Estimated Cost of Completion and Disposal No. Normal...

Benicio also wants to make it easy to access more detailed information about the managers, which he has stored in a Word document. Create a link to a file as follows: a. In cell I9, create a link to...