Show that for a Hamiltonian of the form [H=-G sum_{m, m^{prime}>0} a_{m^{prime}}^{dagger} a_{-m^{prime}}^{dagger} a_{-m} a_{m}] the energy
Question:
Show that for a Hamiltonian of the form
\[H=-G \sum_{m, m^{\prime}>0} a_{m^{\prime}}^{\dagger} a_{-m^{\prime}}^{\dagger} a_{-m} a_{m}\]
the energy eigenvalues for the quasispin model of Problem 31.1 are given by
\[E=G\left(S(S+1)+\frac{1}{4}(N-\Omega)^{2}+\frac{1}{2}(N-\Omega)\right)\]
where $N$ is half the particle number, $\Omega=\frac{1}{2}(2 j+1)$ is half the shell degeneracy, and $S(S+1)$ is the eigenvalue of the operator
\[S^{2}=\frac{1}{2} \sum_{m>0}\left(s_{+}^{(m)} s_{-}^{(m)}+s_{-}^{(m)} s_{+}^{(m)}+s_{0}^{(m)} s_{0}^{(m)}\right)\]
corresponding to the total quasispin.
Data from Problem 31.1
Shell models are important in various fields of physics. Consider a shell of fermions consisting of $(2 j+1)$ degenerate levels of angular momentum $j$, with each level labeled by a projection quantum number $m$ (this is often called a "single $j$-shell model"). Define the fermion operators for a fixed angular momentum $j$ as
\[ s_{+}^{(m)}=a_{m}^{\dagger} a_{-m}^{\dagger} \quad s_{-}^{(m)}=a_{-m} a_{m} \quad s_{0}^{(m)}=\frac{1}{2}\left(a_{m}^{\dagger} a_{m}+a_{-m}^{\dagger} a_{-m}-1\right), \]
where $a_{m}^{\dagger}$ and $a_{m}$ are the usual fermion creation and annihilation operators, respectively, obeying anticommutation relations of the form (3.23). Show that these operators (called quasispin or pseudospin operators) close under
\[ \left[s_{+}^{(m)}, s_{-}^{(m)}\right]=2 s_{0}^{(m)} \quad\left[s_{0}^{(m)}, s_{ \pm}^{(m)}\right]= \pm s_{ \pm}^{(m)} \]
which is the $\mathrm{SU}(2)$ commutator algebra. Quasispin models are of physical relevance for fermion shells exhibiting a strong tendency for pairs of particles to couple to zero total angular momentum. Such models and their generalizations have found substantial application in nuclear, atomic, and condensed matter physics.
Data from 3.23
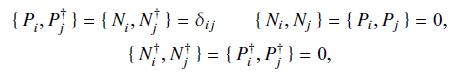
Step by Step Answer:

Symmetry Broken Symmetry And Topology In Modern Physics A First Course
ISBN: 9781316518618
1st Edition
Authors: Mike Guidry, Yang Sun





