Show that the group {e, a, b, c} with multiplication table (b) below, is in one to one correspondence with the geometrical symmetry operations on figure (a) below

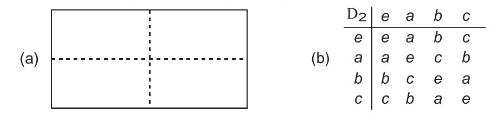
This is called the 4-group or dihedral group \(\mathrm{D}_{2}\). Show that \(\mathrm{D}_{2}\) has three subgroups, \(\{e, a\},\{e, b\}\), and \(\{e, c\}\), each isomorphic to the cyclic group \(\mathrm{C}_{2}\).

(a) D2 e Ce DDC a b c b COD b e e a (b) a a e b b C e a DO C b a