The scatterplot shows the relationship between socioeconomic status measured as the percentage of children in a neighborhood receiving reduced-fee lunches at school (lunch) and the percentage of bike riders in the neighborhood wearing helmets (helmet). The average percentage of children receiving reduced-fee lunches is 30.8% with a standard deviation of 26.7% and the average percentage of bike riders wearing helmets is 38.8% with a standard deviation of 16.9%.

(a) If the R² for the least-squares regression line for these data is 72%, what is the correlation between lunch and helmet?

(b) Calculate the slope and intercept for the least-squares regression line for these data.

(c) Interpret the intercept of the least-squares regression line in the context of the application.

(d) Interpret the slope of the least-squares regression line in the context of the application.

(e) What would the value of the residual be for a neighborhood where 40% of the children receive reduced-fee lunches and 40% of the bike riders wear helmets? Interpret the meaning of this residual in the context of the application.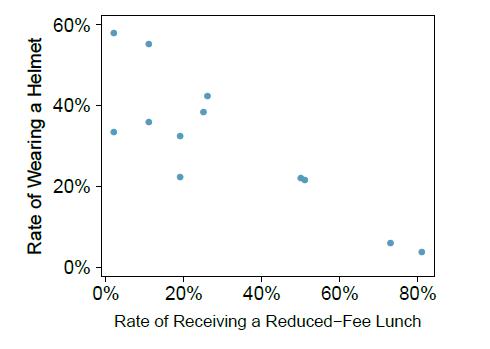

Rate of Wearing a Helmet 60% 40% 20% 0% 0% 20% 40% 60% 80% Rate of Receiving a Reduced-Fee Lunch