The time average of some function Æ’(t) taken over an interval T is given by

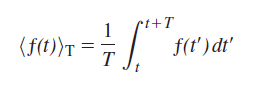
where t' is just a dummy variable. If τ = 2π/ω is the period of a harmonic function, show that vector r.

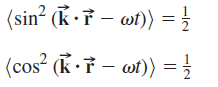
and

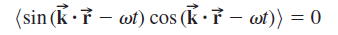
when T = Ï„ and when T > > Ï„.

ri+T f(t') dt' (f(t))T (sin (K F wt)) =} |(cos (Ki - ot)) = }