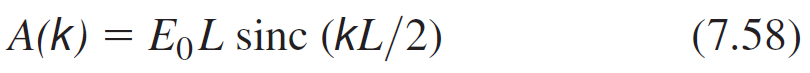
With the last two problems in mind, show that F (1 2 Iuml ) Atilde sinc (1 2 x) rect( Icirc ordm ), starting with the knowledge that F rect(x) sinc (1 2 Icirc ordm ), in other words, Eq (7 58) with L a, where a 1 A(k) E,L sinc (kL 2) (7 58)

Question: With the last two problems in mind, show that F{(1/2Ï) Ã sinc (1/2 x)} = rect(Îº), starting with the knowledge that F{rect(x)} = sinc (1/2

With the last two problems in mind, show that F{(1/2Ï€) Ã— sinc (1/2 x)} = rect(Îº), starting with the knowledge that F{rect(x)} = sinc (1/2 Îº), in other words, Eq. (7.58) with L = a, where a = 1.

A(k) = E,L sinc (kL/2) (7.58)

Step by Step Solution

★★★★★

3.34 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

from Problem ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Optics Questions!

With the last two problems in mind, draw a plot of the three functions (a) sin (b) sin ( - 3/4) (c) sin + sin ( - 3/4). Compare the amplitude of the combined function (c) in this case with that of...

With the previous two problems in mind, imagine a selfluminous object on the central axis of a thin positive lens. The object is a distance d from the screen on which the image appears. Now suppose...

With the previous two problems in mind, compute the magnification that results when the image of a flower 4.0 m from the center of a solid, clear-plastic sphere with a 0.20-m diameter (and a...

Applied Mathematics and Computation 95 (1998) 181192 Love dynamics: The case of linear couples Sergio Rinaldi 1 Centro Teoria dei Sistemi, CNR, Politecnico di Milano, Via Ponzio 34/5, 20133 Milan,...

Providing Quality School-Based Learning and Support Services 239 Chapter 6 Language and literacy support Your core task The core task of almost all TAs is to support students language and literacy...

Each Monday, your professor randomly assigns the 5 problems on the previous week's assignment to a random student to be worked on the board. Students are called in problem order (i.e., the first...

Culhu Company: Transportation Method -. Backorders Permitted Regular Prod. Cost =$7/ init Overtime Prod, Cost =$11/ unit Subcontracting Cost =$15/ unit inventory Cost =$3/ univatr Backordering Cost =...

Q Ch 26:.. Q EXA Question 2 1 pts A paint manufacturer wished to compare the drying times of two different types of paint. Independent simple random samples of 11 cans of Best Paint has a mean drying...

really need help with these questions, thank you! Problem #3 Ashley, being a recent college graduate, has also begun paying off her student loans. She has the following loans when she begins...

Ashley, being a recent college graduate, has also begun paying off her student loans. She has the following loans when she begins repayment: Set 1: $16,200, interest rate 4.45%, paid off over 10...

Why does the gravitational attraction between the Sun and Mercury vary? Would it vary if the orbit or Mercury were perfectly circular?

Sketch a graph of: f(x) = 2 - 1 - 2 1 5- -15 -4 -3 -2 -1 Clear All Draw: 4 3 2 -1 -3 -4 -5 P 3 -

What method would a startup likely use to borrow funds for initial operations? Selling merchandise Public stock offerings Securing a bank loan Reinvesting initial sales profits

If you have to pay off an effective 6.5% loan within the standard 30 years, then what are the per-month payments for the $1,000,000 mortgage? As in Question 3.26, consider both an effective 6.5%...

Consider a classical simple harmonic oscillator (e.g., the nanomechanical oscillator, LIGO mass on an optical spring, L-C-R circuit, or optical resonator briefly discussed in Ex. 6.17). Let the...

Consider an electron that can transition between two levels by emitting or absorbing a photon; and recall that we have argued that the stimulated transitions should be microscopically reversible....

(a) Write down the explicit form of the Langevin equation for the x component of velocity v(t) of a dust particle interacting with thermalized air molecules. (b) Suppose that the dust particle has...

Hello I need to find this using excel please AAA Corp. is comparing two different capital structures. Plan I would result in 12,700 shares of stock and $100,050 in debt. Plan II would result in 9800...

Consider the Finapres data from Recall that the blood pressure of babies was measured using two different methods. The question being asked is about the mean difference between the two measures taken...

People use several methods to keep track of appointments, meetings, and deadlines. Some of these are using a desk calendar, using informal notes of scrap paper, keeping them in your head, using a day...