Consider a system of linear inequalities Ax ≤  b, with A ∈ R^m,n, where a_i^T , i = 1, . . . ,m, denote the rows of A, which are assumed, without loss of generality, to be nonzero. Each inequality a^T_i x ≤ bi can be normalized by dividing both terms by , hence we shall further assume without loss of generality that Consider now the case when the polyhedron described by these inequalities,  is nonempty, that is, there exist at least a point In order to find a feasible point (i.e., a point in P), we propose the following simple algorithm. Let k denote the iteration number and initialize the algorithm with any initial pointholds for all i = 1, . . . ,m, then we found the desired point, hence we return xk, and finish. If instead there exist i_k such that a_ik^T x_k > b_ik , then we set 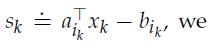we update36 the current point as

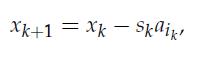
and we iterate the whole process.
1. Give a simple geometric interpretation of this algorithm.
2. Prove that this algorithm either finds a feasible solution in a finite number of iterations, or it produces a sequence of solutions {x_k} that converges asymptotically (i.e., for k → ∞) to a feasible solution (if one exists).
3. The problem of finding a feasible solution for linear inequalities can be also put in relation with the minimization of the nonsmooth function Develop a sub gradient type algorithm for this version of the problem, discuss hypotheses that need be assumed to guarantee convergence, and clarify the relations and similarities with the previous algorithm.

||ai||2,