Question: Consider a constrained minimization problem where f 0 is convex and smooth and is convex and compact. Clearly, a projected gradient or proximal gradient algorithm
Consider a constrained minimization problem
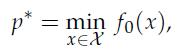
where f0 is convex and smooth and ![]() is convex and compact. Clearly, a projected gradient or proximal gradient algorithm could be applied to this problem, if the projection onto X is easy to compute. When this is not the case, the following alternative algorithm has been proposed.
is convex and compact. Clearly, a projected gradient or proximal gradient algorithm could be applied to this problem, if the projection onto X is easy to compute. When this is not the case, the following alternative algorithm has been proposed.
Initialize the iterations with some ![]() Determine the gradient
Determine the gradient ![]() and solve
and solve
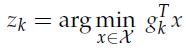
Then, update the current point as.
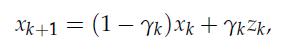
where![]() and, in particular, we choose
and, in particular, we choose
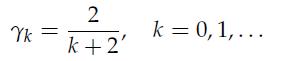
Assume that f0 has a Lipschitz continuous gradient with Lipschitz
constant L, and that ![]() for every x, y ∈ X. In this. exercise, you shall prove that
for every x, y ∈ X. In this. exercise, you shall prove that
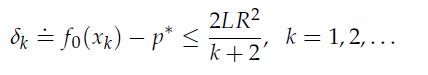
1. Using the inequality
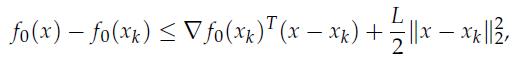
which holds for any convex f0 with Lipschitz continuous gradient, prove that
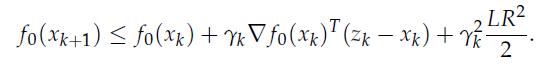
2. Show that the following recursion holds for δk:
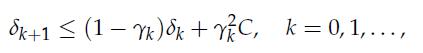 for
for ![]()
3. Prove by induction on k the desired result (12.27).
p* = min fo(x), XEX
Step by Step Solution
3.38 Rating (157 Votes )
There are 3 Steps involved in it
1 Using inequality 125 we have that which proves the first po... View full answer

Get step-by-step solutions from verified subject matter experts


