Question: Let X R n + m be a matrix with non-negative entries, and p, r [1, + ], with p r. We

Let X ∈ Rn+m be a matrix with non-negative entries, and p, r ∈  [1, + ∞], with p ≥ r. We consider the problem


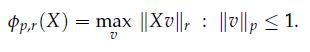
Ppr (X) = max ||XV||||||p 1. V

1. Show that the function fX : Rm+ → R, with values

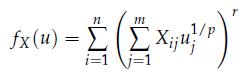
is concave when p ≥ r.

2. Use the previous result to formulate an efficiently solvable convex problem that has Φp,r(X)r as optimal value.

Ppr (X) = max ||XV||||||p 1. V

Step by Step Solution

★★★★★

3.35 Rating (167 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

1 The convexity condition is obvious if p r 1 Let us assume r 1 The function f is twice differ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Optimization Models Questions!

Q:

Let A be a matrix with eigenvalues λ1. . . . . . λn and let λ be an eigenvalue of A + E. Let X be a matrix that diagonalizes A and let C = X-1EX. Prove (a) For...

Q:

Let A be a matrix with linearly independent columns. Prove the following: (a) (cA)+ = ( l/c)A+ for all scalars c 0. (b) (A+)+ = A if A is a square matrix. (c) (AT)+ = (A+)T if A is a square matrix.

Q:

Let A be a matrix with integer entries. If | det(A) | = 1, then what can you conclude about the nature of the entries of A-1? Explain.

Q:

Let (x): R R be a non-negative function, so that f(x)dx = 1. Show that for any continuous function f : RR, we have that the sequence In(x) = n (n(x-y))f(y)dx converges uniformly on the compact sets...

Q:

Provide detailed information Question 2 When we studied consumer theory in ECN200A, we introduced various functions like utility functions, indirect utility functions, expenditure functions,...

Q:

In this question assume that p and q are atomic formulae. (a) Compare and contrast path formulae and state formulae in temporal logic. [4 marks] (b) Describe and contrast the meanings of F(G p) and...

Q:

,, kindly solve Consider the Linear Regression Model 1. For any X = x, let Y = x8 + U, where B E R*. 2. X is exogenous. 3. The probability model is { f (u; ) is a distribution on R : E, [U] = 0, Var,...

Q:

Please help with these questions 1. Let the inner product in a linear subspace V C R" be defined as V= X'AY where matrix A is positive definite. Please show that P is an orthogonal projector if and...

Q:

Recall that N is the set of positive integers and Q is the set of rational numbers. NOTE: "Limit point\Sequences - Part 2 (Week 4) Infinite Limits Definition. A sequence (sn) is said to diverge to +...

Q:

,.. I need your input here please Amanda's utility function is Leontief and given by Wa(Xarya) = min(xa. yal while Brenda's utility is linear and given by us(xb. )b) = XD + VD Their endowments are wa...

Q:

One conductor of an overhead electric transmission line is a long aluminum wire 2.40 cm in radius. Suppose that at a particular moment it carries charge per length 1.40 C/m and is at potential 345...

Q:

Let E represent global emissions of CO2 from fossil fuel burning and cement. Suppose that the marginal private surplus from emissions (the private surplus from each additional small unit of...

Q:

13.28 In Problem 13.6 on page 470, a prospective MBA student wanted to predict starting salary upon graduation, based on program per-year tuition. Perform a residual analysis for these data (stored...

Q:

Throughout the country, the proportion of first time, first-year community college students who return for their second year of studies is 0.52 according to the Community College Survey of Student...

Q:

Use these dataincidents of reports of underage drinkingto perform the following: Dry campus, state school: 47, 52, 27, 50 Dry campus, private school: 25, 33, 31 Wet campus, state school: 77, 61, 55,...

Q:

Using what you know about the expanded source table, fill in the missing values in the table shown here: df Source SS MS Gender 248.25 Parenting style 84.34 33.60 Gender X style Within 1107.2 36...

Q:

Using the information in the source table provided here, compute R 2 values for each effect. Using Cohens conventions, explain what these values mean. df Source SS MS A (rows) 0.267 0.267 0.004 B...

Q:

Valuation fundamentals Personal Finance Problem Imagine that you are trying to evaluate the economics of purchasing a condominium to live in during college rather than renting an appartment. If you...

Q:

Suppose you collected the following financial information from various sources: Financial information as of July 2022 a Based on the information provided in the table above, compute the theoretical...

Q:

Financial analysts forecast L Brands (LB) growth for the future to be 13.8 percent. LB's most recent dividend was $2.40. What is the fair present value of L Brands's stock if the required rate of...