We are given a data matrix X = [x⁽¹⁾, . . . , x^(m)], with x⁽ⁱ⁾ ∈ Rⁿ, i = 1, . . . ,m. We assume that the data is centered: x⁽¹⁾ + . . . + x^(m) = 0. An (empirical) estimate of the covariance matrix is

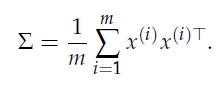
In practice, one often finds that the above estimate of the covariance matrix is noisy. One way to remove noise is to approximate the covariance matrix as , where F is a n x k matrix, containing the so-called “factor loadings,” with k

x = F f + σ_e,

where x is the (random) vector of centered observations, (f , e) is a random variable with zero mean and unit covariance matrix, and σ = √λ is the standard deviation of the idiosyncratic noise component σ_e. The interpretation of the stochastic model is that the observations are a combination of a small number k of factors, plus a noise part that affects each dimension independently. To fit F, λ to data, we seek to solve

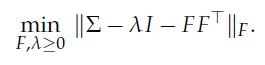
1. Assume l is known and less than λ_k (the k-th largest eigenvalue of the empirical covariance matrix ∑). Express an optimal F as a function of λ, which we denote F(λ). In other words: you are asked to solve for F, with fixed λ.

2. Show that the error the matrix you found in the previous part, can be written as 

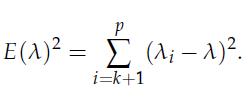
Find a closed-form expression for the optimal l that minimizes the error, and summarize your solution to the estimation problem (13.35).

3. Assume that we wish to estimate the risk (as measured by variance) involved in a specific direction in data space. Recall from Example 4.2 that, given a unit-norm n-vector w, the variance along direction ω is ω^T ∑ω. Show that the rank-k approximation to S results in an under-estimate of the directional risk, as compared with using ∑. How about the approximation based on the factor model above? Discuss.

M 1 m [x(i) x(i) T m i=1