We have a historical data set containing the values of a times series r(1), . . . , r(T). Our goal is to predict if the time-series is going up or down. The basic idea is to use a prediction based on the sign of the output of an auto-regressive model that uses n past data values (here, n is fixed). That is, the prediction at time t of the sign of the value r(t +1) – r(t) is of the form

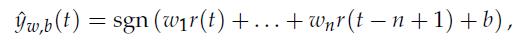
In the above, ω ∈ Rⁿ is our classifier coefficient, b is a bias term, and n

1. As a first attempt, we would like to solve the problem

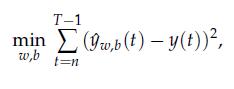
where y(t) = sgn(r(t + 1) – r(t)). In other words, we are trying to match, in a least-squares sense, the prediction made by the classifier on the training set, with the observed truth. Can we solve the above with convex optimization? If not, why?

2. Explain how you would set up the problem and train a classifier using convex optimization. Make sure to define precisely the learning procedure, the variables in the resulting optimization problem, and how you would find the optimal variables to make a prediction.

w,b (t) = sgn (wr(t) +...+wnr(t n + 1) + b),