We are given m data points and we seek an hyperplane  where and that best “fits” the given points, in the sense of a minimum sum of squared distances criterion.

Formally, we need to solve the optimization problem

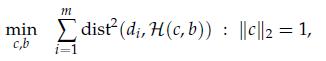
where dist is the Euclidean distance from a point d to . Here the constraint on c is imposed without loss of generality, in a way that does not favor a particular direction in space.

1. dShow that the distance from a given pointis given by

2. Show that the problem can be expressed as

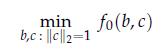
where f₀ is a certain quadratic function, which you will determine.

3. Show that the problem can be reduced to

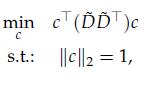
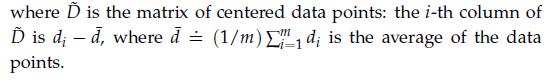
4. Explain how to find the hyperplane via SVD.

d,..., dm R,