We consider a multi-stage, single-asset investment decision problem over n periods. For any given time period i = 1 ,..., n, we denote by y_i the predicted return, σ_i the associated variance, and u_i the dollar position invested. Assuming our initial position is u₀ = ω, the investment problem is

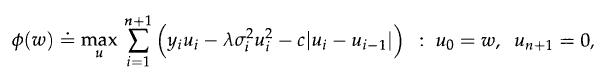
where the first term represents profit, the second, risk, and the third, approximate transaction costs. Here, c > 0 is the unit transaction cost and λ > 0 a risk-return tradeoff parameter. (We assume λ = 1 without loss of generalityΙ.)

1. Find a dual for this problem.
2. Show that (ϕ is concave, and find a subgradient of — ϕ at ω. If (p is differentiable at ω, what is its gradient at ω?

3. What is the sensitivity issue of (p with respect to the initial position w? Precisely, provide a tight upper bound on Ιϕ(ω + ϵ) — ϕ(ω)Ι for arbitrary ϵ > 0, and with y, σ, c fixed. You may assume ϕ is differentiable for any u ∈ [ω,ω + ϵ].

ML1 () = max (yu u c\u; u;-1) -c\ui 21 ui-1\) : uo = w, un+1 = 0,