We consider the problem where is a regularization parameter, and 0 allows to control the cardinality (number of non-zeros) in the solution. This

We consider the problem

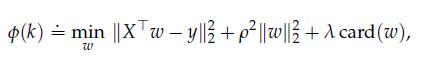
where is a regularization parameter, and λ ≥ 0 allows to control the cardinality (number of non-zeros) in the solution. This in turn allows better interpretability of the results. The above problem is hard to solve in general. In the sequel, we denote by a_i^T , i = 1, . . . , n the i-th row of X, which corresponds to a particular “feature” (that is, dimension of the variable ω).

1. First assume that no cardinality penalty is present, that is, λ = 0. Show that

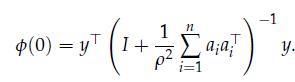
2. Now consider the case l > 0. Show that

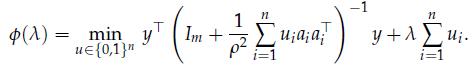
3. A natural relaxation to the problem obtains upon replacing the constraints u ∈ {0, 1}ⁿ with interval ones: u ∈ [0, 1]ⁿ. Show that the resulting lower bound Φ(λ) ≥ Φ(λ) is the optimal value of the convex problem

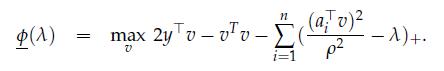
How would you recover a sub-optimal sparsity pattern from a solution v to the above problem?

4. Express the above problem as an SOCP.

5. Form a dual to the SOCP, and show that it can be reduced to the expression

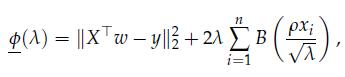
where B is the (convex) reverse Hüber function: for  

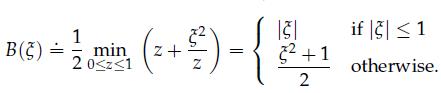
Again, how would you recover a sub-optimal sparsity pattern from a solution w to the above problem?

6. A classical way to handle cardinality penalties is to replace them with the ℓ1-norm. How does the above approach compare with the ℓ1-norm relaxation one? Discuss.

p(k) = min ||Xw-y||2+p||w||2+ A card (w), W