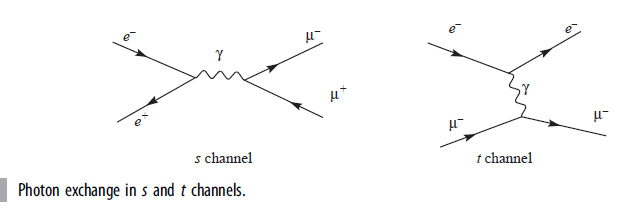
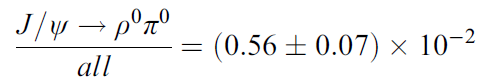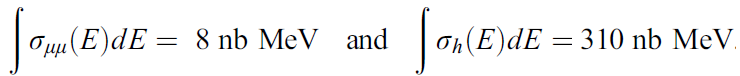![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


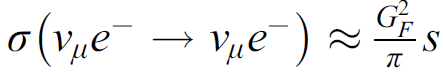
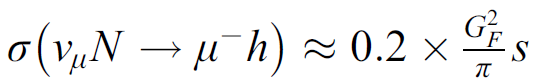
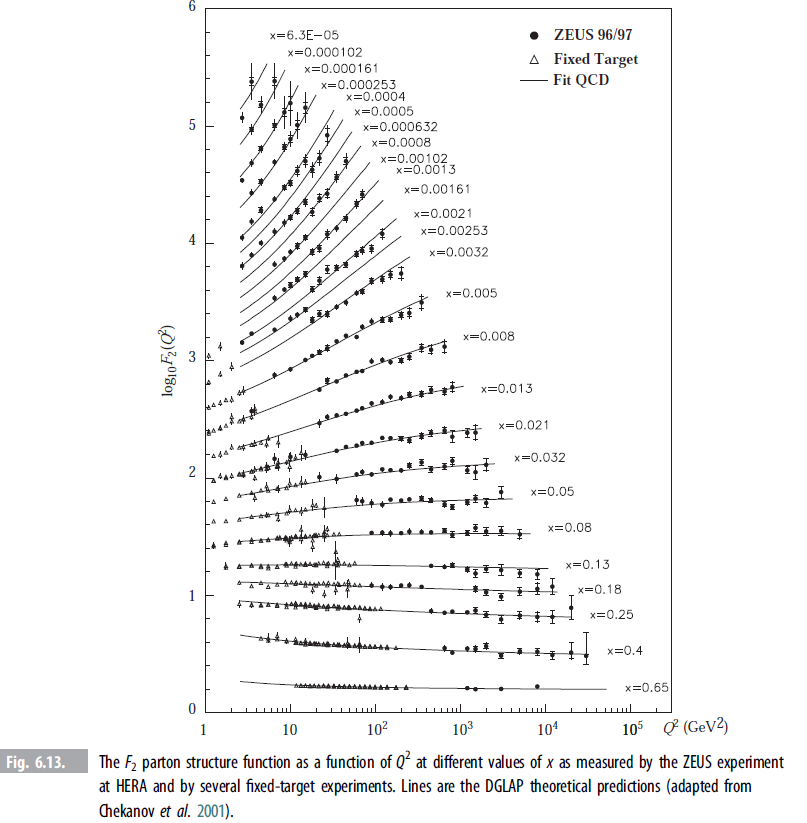
![E' = E/[1+(1 – cos 0)]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1547/1/2/6/2475c3745e7de4341547108874927.jpg)