a. Draw a figure like the one in Exercise 83 for a continuous function (x) whose values decrease steadily as x moves from left to

a. Draw a figure like the one in Exercise 83 for a continuous function ƒ(x) whose values decrease steadily as x moves from left to right across the interval [a, b]. Let P be a partition of [a, b] into subintervals of equal length. Find an expression for U - L that is analogous to the one you found for U - L in Exercise 83a.

b. Suppose that instead of being equal, the lengths Δxk of the subintervals of P vary in size. Show that the inequality

of Exercise 83b still holds and hence that

(U - L) = 0.

Exercise 83

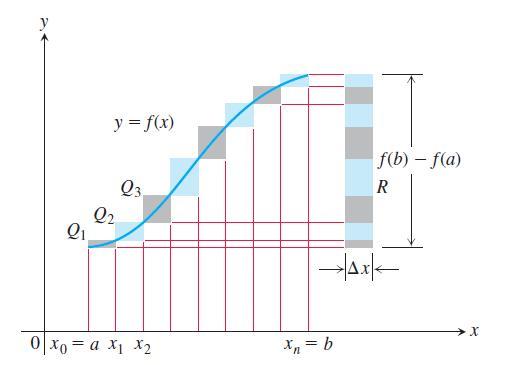
a. Suppose the graph of a continuous function ƒ(x) rises steadily as x moves from left to right across an interval [a, b]. Let P be a partition of [a, b] into n subintervals of equal length Δx = (b - a)/n. Show by referring to the accompanying figure that the difference between the upper and lower sums for ƒ on this partition can be represented graphically as the area of a rectangle R whose dimensions are [ƒ(b) - ƒ(a) ] by Δx.

b. Suppose that instead of being equal, the lengths Δxk of the subintervals of the partition of [a, b] vary in size. Show that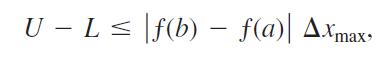

where Δx_max is the norm of P, and hence that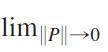

(U - L) = 0.

Q y = f(x) Q2 Q3 0|xo = a X X xn = b f(b) - f(a) R X