Suppose that is the differentiable function shown in the accompanying graph and that the position at time t (sec) of a particle moving along

Suppose that ƒ is the differentiable function shown in the accompanying graph and that the position at time t (sec) of a particle moving along a coordinate axis is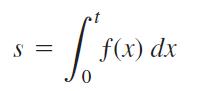

meters. Use the graph to answer the following questions. Give reasons for your answers.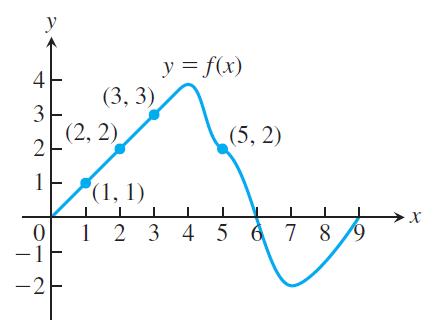

a. What is the particle’s velocity at time t = 5?

b. Is the acceleration of the particle at time t = 5 positive, or negative?

c. What is the particle’s position at time t = 3?

d. At what time during the first 9 sec does s have its largest value?

e. Approximately when is the acceleration zero?

f. When is the particle moving toward the origin? Away from the origin?

g. On which side of the origin does the particle lie at time t = 9?

S = 0 f(x) dx