A frictionless particle P, starting from rest at time t = 0 at the point (a, 0, 0), slides down the helix

under the influence of gravity, as in the accompanying figure. The θ in this equation is the cylindrical coordinate θ and the helix is the curve r = a, z = bθ, θ ≥ 0, in cylindrical coordinates. We assume θ to be a differentiable function of t for the motion. The law of conservation of energy tells us that the particle’s speed after it has fallen straight down a distance z is √2gz, where g is the constant acceleration of gravity.

a. Find the angular velocity dθ/dt when θ = 2π.

b. Express the particle’s θ- and z-coordinates as functions of t.

c. Express the tangential and normal components of the velocity dr / dt and acceleration d²r/dt² as functions of t. Does the acceleration have any nonzero component in the direction of the binormal vector B?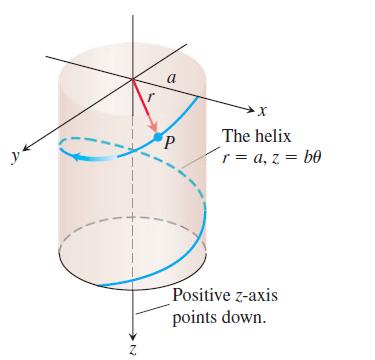

r(0) = (a cos 0)i + (a sin 0)j + bok (a, b > 0)