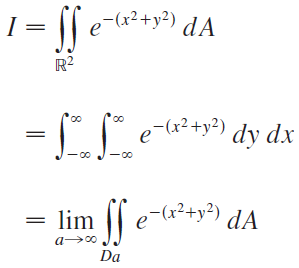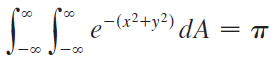
(a) We define the improper integral (over the entire plane R 2 d) where D a is the disk with radius a and center the origin Show that (b) An equivalent definition of the improper integral in part (a) is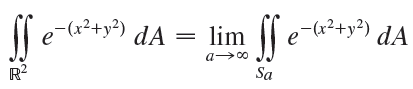 where S a is the square with vertices (a, a) Use this to show that 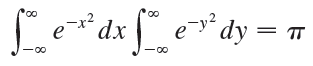(c) Deduce that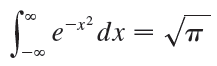 (d) By making...

Mathematics
Precalculus
(a) We define the improper integral (over the entire plane

(a) We define the improper integral (over the entire plane R 2 d) where D a is the disk with...

Question:

(a) We define the improper integral (over the entire plane R²d) le-42+y?) dA -(x²+y²) -Se-ta?4y?, R2 -(x²+y²) dy dx - 00 -00 -(x²+y²) = lim dA Da where D_a is the disk with radius a and center the origin. Show that

e-(x²+y²) dA = T o,

(b) An equivalent definition of the improper integral in part (a) iswhere S_a is the square with vertices (±a, ±a). Use this to show that

(d) By making the change of variable t = √2 x, show that

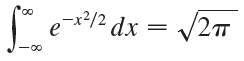
(This is a fundamental result for probability and statistics.)

Transcribed Image Text:

le-42+y?) dA -(x²+y²) -Se-ta?4y?, R2 -(x²+y²) dy dx - 00 -00 -(x²+y²) = lim dA Da e-(x²+y²) dA = T o,

This problem has been solved!

Do you need an answer to a question different from the above? Ask your question!

Step by Step Answer:

Answer rating: 57% (7 reviews)

2 a SSD e v dA rer dr d0 2 e r n 1 e for each a Then lim …View the full answer

Answered By

Zablon Gicharu

I am an educator who possesses the requisite skills and knowledge due to interacting with students for an extended period. I provide solutions to various problems in step-by-step explanations, a well-thought approach and an understandable breakdown. My goal is to impart more straightforward methodologies and understanding to students for more remarkable achievements.

5.00+ 4+ Reviews 10+ Question Solved

Related Book For answer-question