Assume that an ice cube retains its cubical shape as it melts. If we call its edge length s, its volume is V = s³ and its surface area is 6s². We assume that V and s are differentiable functions of time t. We assume also that the cube’s volume decreases at a rate that is proportional to its surface area. (This latter assumption seems reasonable enough when we think that the melting takes place at the surface: Changing the amount of surface changes the amount of ice exposed to melt.) In mathematical terms,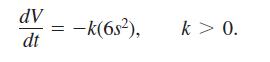

The minus sign indicates that the volume is decreasing. We assume that the proportionality factor k is constant. (It probably depends on many things, such as the relative humidity of the surrounding air, the air temperature, and the incidence or absence of sunlight, to name only a few.) Assume a particular set of conditions in which the cube lost 1/4 of its volume during the first hour, and that the volume is V₀ when t = 0. How long will it take the ice cube to melt?

dv dt -k(6s), k > 0.